Examples for secondary school students - page 75 of 231
Number of problems found: 4610
- Subjected 37351
 The football player kicked a 400 g ball with a force of 480 N during a penalty. How fast did the ball again if it was subjected to an impact force of 0.01 s?
The football player kicked a 400 g ball with a force of 480 N during a penalty. How fast did the ball again if it was subjected to an impact force of 0.01 s? - Seeds
 The germination of seeds of a certain species of carrot is 96%. What is the probability that at least 25 seeds out of 30 will germinate?
The germination of seeds of a certain species of carrot is 96%. What is the probability that at least 25 seeds out of 30 will germinate? - Parametric equation
 Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 >
Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 > - Oscillating 37271
 Calculate the oscillation time T of the undamped harmonic oscillating motion of a particle of mass m = 10 g if the force holding the particle in this motion has a value of F = 0,05 N at a deflection of x = 3 cm.
Calculate the oscillation time T of the undamped harmonic oscillating motion of a particle of mass m = 10 g if the force holding the particle in this motion has a value of F = 0,05 N at a deflection of x = 3 cm. - Instantaneous 37201
 The amplitude of the linear undamped harmonic oscillator is A = 12 cm, and the frequency f = 15 Hz. What is its instantaneous deflection at time a) t1 = 0.02s, b) t2 = 0.04s, when it was zero at time t = 0 s?
The amplitude of the linear undamped harmonic oscillator is A = 12 cm, and the frequency f = 15 Hz. What is its instantaneous deflection at time a) t1 = 0.02s, b) t2 = 0.04s, when it was zero at time t = 0 s? - Annual growth
 The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was.
The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was. - Depreciated 37171
 The initial price of the machine is 23,000 euros. Every year, 12% of its cost is depreciated due to wear and tear. What value will the machine have after six years?
The initial price of the machine is 23,000 euros. Every year, 12% of its cost is depreciated due to wear and tear. What value will the machine have after six years? - Withdraw 37161
 We will deposit € 8,500 into the bank at 1.3% interest and withdraw € 8,700. How many years do we have to wait? Round to 2 decimal places.
We will deposit € 8,500 into the bank at 1.3% interest and withdraw € 8,700. How many years do we have to wait? Round to 2 decimal places. - Possibilities 36911
 There are seven fountains in the city. Only five always work. How many possibilities do five fountains work at the same time?
There are seven fountains in the city. Only five always work. How many possibilities do five fountains work at the same time? - Arithmetic 36901
 The examiner has prepared 20 examples from arithmetic. He wants to choose seven samples for the paper. The order of the examples does not matter. How many different papers can he compile?
The examiner has prepared 20 examples from arithmetic. He wants to choose seven samples for the paper. The order of the examples does not matter. How many different papers can he compile? - Different 36891
 We put seven different things out of fifteen various goods in the shopping cart. How many cart content options occur?
We put seven different things out of fifteen various goods in the shopping cart. How many cart content options occur? - Students 36881
 As a reward, the trip's land is ten students from a class of 25 students. How many options are there?
As a reward, the trip's land is ten students from a class of 25 students. How many options are there? - Books - triplets
 I will choose three from ten different books. How many different triplets can I choose?
I will choose three from ten different books. How many different triplets can I choose? - Common difference
 The 4th term of an arithmetic progression is 6. Find the common difference if the sum of the 8th and 9th terms is -72.
The 4th term of an arithmetic progression is 6. Find the common difference if the sum of the 8th and 9th terms is -72. - Mappings of complex numbers
 Find the images of the following points under mappings: z=3-2j w=2zj+j-1
Find the images of the following points under mappings: z=3-2j w=2zj+j-1 - Half-planes 36831
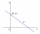 The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest.
The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest. - Warehouse 36811
 At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev
At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev - Annual increase
 The number of cars produced increased from 45,000 to 47,000 in 3 years. Calculate the average annual increase in cars in%.
The number of cars produced increased from 45,000 to 47,000 in 3 years. Calculate the average annual increase in cars in%. - Compressed gas
 The pressure vessel contains a compressed gas at a temperature t1 = 27°C and a pressure p1 = 4 MPa. How much does its pressure change when we release half the amount of gas, and its temperature drops to t2 = 15°C?
The pressure vessel contains a compressed gas at a temperature t1 = 27°C and a pressure p1 = 4 MPa. How much does its pressure change when we release half the amount of gas, and its temperature drops to t2 = 15°C? - A mountain climber
 A mountain climber plans to buy some rope to use as a lifeline. Which of the following would be the better choice? Explain your choice. Rope A: Mean breaking strength:500lb; the standard deviation of 100lb Rope B: Mean breaking strength: 500lb; the standa
A mountain climber plans to buy some rope to use as a lifeline. Which of the following would be the better choice? Explain your choice. Rope A: Mean breaking strength:500lb; the standard deviation of 100lb Rope B: Mean breaking strength: 500lb; the standa
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
