Isolating a variable in the formula - math word problems - page 132 of 144
Number of problems found: 2871
- Cuboid - edges
The cuboid has dimensions in a ratio of 4:3:5. The shortest edge is 12 cm long. Find: The lengths of the remaining edges The surface of the cuboid The volume of the cuboid - Hexagonal prism 2
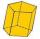The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume. - Calculated 3465
The master calculated that six looms would weave the ordered fabric in 15 hours. One condition appeared. How long before the ordered substance matches the remaining states? - Pyramid in cube
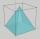In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid. - The tent
The tent shape of a regular quadrilateral pyramid has a base edge length of a = 2 m and a height of v = 1.8 m. If we have to add 7% of the seams, how many m² of cloth did we need to make the tent? How many m³ of air will be in the tent? - Cube walls
Find the volume and surface area of the cube if the area of one wall is 40 cm². - Rotary bodies
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
- The gardener
The gardener bought trees for 960 CZK. If every tree were cheaper by 12 CZK, he would have gotten four more trees for the same money. How many trees did he buy? - RT perimeter
The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference. - Subsequent 3427
Find how many strings there are in the first row if there are 44 strings in the eighth row, and in each subsequent row, there are five more strings than in the previous row. - Rectangle from string
String 12m. Make a rectangle when one side is two times longer than its width. - Wall height
Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm. - Axial cut
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume. - Cylindrical 3394
The cylindrical container with a diameter of 1.8 m contains 2000 l of water. What height does the water reach? - Cube diagonals
If you know the length of the body diagonal u = 216 cm, determine the cube's volume and surface area.
- Wednesday 3391
On Monday, three pupils were missing from the class, 12% of the total number of pupils. How many pupils were missing on Wednesday if 84% of all pupils were in school? - Pyramid
The pyramid has a base rectangle with a = 6cm and b = 8cm. The side edges are the same, and their length is 12.5 cm. Calculate the surface of the pyramid. - Cuboid and ratio
A cuboid has dimensions in a ratio of 1:2:6, and the surface area of the cuboid is 1000 dm². Calculate the volume of the cuboid. - Cylindrical tank
The cylindrical tank holds 600hl water and is deep 2.5 m. Calculate the diameter of the cylinder. - Electrons 3363
How many electrons must be together to put a charge of -1C together?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
