Isolating a variable in the formula - math word problems - page 59 of 145
Number of problems found: 2890
- Circumference 30761
 There is 0.3 dl of strawberry ice cream in the cone-shaped ice cream cone. Calculate the depth of the cornet if its circumference is 5.6 cm.
There is 0.3 dl of strawberry ice cream in the cone-shaped ice cream cone. Calculate the depth of the cornet if its circumference is 5.6 cm. - Cube V2S
 The volume of the cube is 27 dm cubic. Calculate the surface of the cube.
The volume of the cube is 27 dm cubic. Calculate the surface of the cube. - Sphere parts, segment
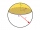 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment? - Area and perimeter of rectangle
 The rectangle area is 3000 cm2, and one dimension is 10 cm larger than the other. Determine the perimeter of the rectangle.
The rectangle area is 3000 cm2, and one dimension is 10 cm larger than the other. Determine the perimeter of the rectangle. - The volume
 The volume of the sphere is 1 m³. What is its surface?
The volume of the sphere is 1 m³. What is its surface? - Regular quadrilateral pyramid
 What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm?
What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm? - Isosceles trapezoid
 Find the area of an isosceles trapezoid; if the bases are 12 cm and 20 cm, the arm's length is 16 cm.
Find the area of an isosceles trapezoid; if the bases are 12 cm and 20 cm, the arm's length is 16 cm. - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Vertical rod
 The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously.
The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously. - Millimeter 30041
 Calculate the length of the wall diagonal of a cube with a volume of 7.40 dm cubic. Express the result to the nearest millimeter.
Calculate the length of the wall diagonal of a cube with a volume of 7.40 dm cubic. Express the result to the nearest millimeter. - Kilometers 30021
 The first group of tourists left the hut at 8:00 AM at a speed of 4 km/h. The second group of tourists followed them half an hour later at a speed of 6 km/h. How long and how many kilometers from the cottage will it catch up with the first group?
The first group of tourists left the hut at 8:00 AM at a speed of 4 km/h. The second group of tourists followed them half an hour later at a speed of 6 km/h. How long and how many kilometers from the cottage will it catch up with the first group? - Thousand balls
 We must create a thousand balls from a sphere with a diameter of 1 m. What will be their radius?
We must create a thousand balls from a sphere with a diameter of 1 m. What will be their radius? - Vertical 29801
 The shadow of the building is 16 m long, and the shadow of the vertical meter rod is 0.8 m long at the same time. What is the height of the building?
The shadow of the building is 16 m long, and the shadow of the vertical meter rod is 0.8 m long at the same time. What is the height of the building? - Volume of sphere
 How many times does the volume of a sphere increase if its radius increases two times?
How many times does the volume of a sphere increase if its radius increases two times? - Cylindrical tank
 9.6 hl of water is poured into a cylindrical tank with a bottom diameter of 1.2 m. What height in centimeters does the water reach?
9.6 hl of water is poured into a cylindrical tank with a bottom diameter of 1.2 m. What height in centimeters does the water reach? - The string
 They cut 113 cm from the string and divided the rest in a ratio of 5:6.5:8:9.5. The longest part measured 38 cm. Find the original length of the string.
They cut 113 cm from the string and divided the rest in a ratio of 5:6.5:8:9.5. The longest part measured 38 cm. Find the original length of the string. - Extending square garden
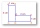 Mrs. Petrová's garden had a square shape with a side length of 15 m. After its enlargement by 64 m² (square), it became a square again. How many meters has the length of each side of the garden been extended?
Mrs. Petrová's garden had a square shape with a side length of 15 m. After its enlargement by 64 m² (square), it became a square again. How many meters has the length of each side of the garden been extended? - Inhabitants 29451
 480 people live in the village of Grandmother. There are seven times fewer blue-eyed people than people with different eye colors. How many inhabitants of the village are blue-eyed?
480 people live in the village of Grandmother. There are seven times fewer blue-eyed people than people with different eye colors. How many inhabitants of the village are blue-eyed? - Sphere in cone
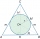 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Quadrilateral pyramid,
 A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid
A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
