Mathematical Olympiad - practice problems - page 4 of 9
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 176
- Divisible 9331
The number X is the smallest natural number whose half is divisible by three, a third is divisible by four, a quarter is divisible by eleven, and its half gives a remainder of 5 when divided by seven. Find this number. - Identical 8831
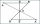In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Determine 8611 Determine all natural numbers A and B pairs for which the sum of twice the least common multiple and three times the greatest common divisor of natural numbers A and B is equal to their product.
- Solutions 8481
For which integers x is the ratio (x + 11) / (x + 7) an integer? Find all solutions. - Justification 8468
The natural number n has at least 73 two-digit divisors. Prove that one of them is the number 60. Also, give an example of the number n, which has exactly 73 double-digit divisors, including a proper justification. - Luggage and air travel
Two friends traveling by plane had a total of 35 kg of luggage. They paid one 72 CZK and the second 108 CZK for being overweight. If only one paid for all the bags, it would cost 300 CZK. What weight of baggage did each of them have? How many kilograms of - Self-counting machine
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he
- Six-digit primes
Find all six-digit prime numbers that contain each one of digits 1,2,4,5,7, and 8 just once. How many are there? - Restriction 7442
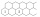The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Inequality 7320
Let a, b, and c be positive real numbers whose sum is 3, each of which is at most 2. Prove that the inequality holds: a2 + b2 + c2 + 3abc - -------------- 7311 In the following additional example, the same letters represent the same digits, and the different letters represent different digits: RATAM RAD -------------- ULOHY Replace the letters with numbers so that the example is correct. Find two different repla
- Single-digit 7302 Four different digits were on the four cards, one of which was zero. Vojta composed the largest four-digit number from the cards, and Martin the smallest four-digit number. Adam wrote the difference between Vojtov's and Martin's numbers on the board. Then
- Parenthesis 7284 Tomas received nine cards with the following numbers and math symbols for math olympiad results. 18, 19, 20, 20, +, -, x, (,) Note 4 numbers and operators plus, minus, times, left parenthesis, right parenthesis. He stored the cards so that there were neve
- Year 2018
The product of the three positive numbers is 2018. What are the numbers? - Three-digit number
Find all three-digit numbers n with three different non-zero digits divisible by the sum of all three two-digit numbers we get when we delete one digit in the original number.
- Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Quadrilaterals II
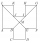In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M and divide the dodecago - Perpendicular sides In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ
- Conditions 7186
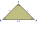Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Ticháček 7185
Mr. Ticháček had three gypsum dwarfs in the garden: the largest was called Maško, the middle Jarko, and the smallest Franko. Since he liked to play with them, he discovered that when he put Fan on Jarek, they were as tall as Maško. On the other hand, when
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
