Quadrilaterals II
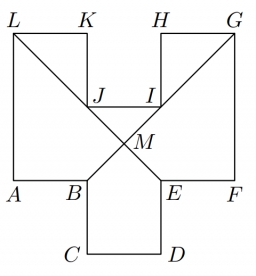
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M and divide the dodecagon into six shapes (three triangles, two quadrilaterals, and one pentagon). The EFGM square has an area of 7 cm2.
Determine the area of the other five departments.
Your answer:
Determine the area of the other five departments.
Your answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetrybasic operations and conceptsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perpendicular sides
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ - Z5 – I – 2 MO 2018
Tereza received four identical right-angled triangles with sides of lengths 3 cm, 4 cm, and 5 cm. From these triangles (not necessarily all four) she tried to put together new shapes. She gradually managed to put together quadrilaterals with perimeters of - Pentagon
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6 dm, | PD | = 8.4 - MO-I-Z6
A square with a side of 4 cm is divided into squares with a side of 1 cm as shown in the figure. Divide the square along the marked lines into two figures each with a perimeter of 16 cm. Find at least three different solutions (i.e. three solutions such t - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Quadrangle ACEG
The figure shows two rectangles ABCD and DEFG, with |DE| = 3 cm, |AD| = 6 cm, |DG| = 5 cm, and |CD| = 10 cm. Calculate the area of quadrilateral ACEG. Figure description: the two rectangles share vertex D. Rectangle ABCD has sides twice as long as those o - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
