Natural numbers - math word problems - page 32 of 92
Number of problems found: 1826
- Email hoard
 Kendrick received 24 fewer e-mails on Friday than he did on Thursday. If he received a total of 126 e-mails on those two days, how many did he get each day?
Kendrick received 24 fewer e-mails on Friday than he did on Thursday. If he received a total of 126 e-mails on those two days, how many did he get each day? - Determines 38523
 We have 30 flowers, and each one has three or four petals. They have a total of 102 chips. How many flowers have four petals? Z represents the number of flowers with 4 petals. Choose the expression that determines the number of flowers with 3 petals.
We have 30 flowers, and each one has three or four petals. They have a total of 102 chips. How many flowers have four petals? Z represents the number of flowers with 4 petals. Choose the expression that determines the number of flowers with 3 petals. - Electric 36771
 There was a gear in the electric mixer. The drive wheel had 24 teeth. The driven wheel had 36 teeth. When did the same teeth of both wheels meet again?
There was a gear in the electric mixer. The drive wheel had 24 teeth. The driven wheel had 36 teeth. When did the same teeth of both wheels meet again? - Bullets 7405
 Pavol, Igor, and Kubo played bullets. They had a total of 25 marbles. Palo had 6 more bullets than Kubo at the start. Then Igor won 8 bullets from Pavol, and thus Igor had the same number of bullets as Kubo. How many marbles does Pal have left?
Pavol, Igor, and Kubo played bullets. They had a total of 25 marbles. Palo had 6 more bullets than Kubo at the start. Then Igor won 8 bullets from Pavol, and thus Igor had the same number of bullets as Kubo. How many marbles does Pal have left? - Establishes 5921
 The boy establishes collections of spiders and beetles. So far, he has only a total of 8. When asked how many beetles he has, he replied: "My entire collection has 54 legs. "How many spiders and how many beetles?
The boy establishes collections of spiders and beetles. So far, he has only a total of 8. When asked how many beetles he has, he replied: "My entire collection has 54 legs. "How many spiders and how many beetles? - Three-digit 4882
 There were 301 postage stamps in the desk drawer. They were stamps for 2, 3, and 5 crowns. The number of each species can be written as a three-digit number. The total price of all stamps is CZK 1,003. How many stamps were there?
There were 301 postage stamps in the desk drawer. They were stamps for 2, 3, and 5 crowns. The number of each species can be written as a three-digit number. The total price of all stamps is CZK 1,003. How many stamps were there? - Pair of numbers
 Hana gave Simon a riddle: guess a pair of numbers whose GCD is 7, and LCM is 90. Katy wanted Simon to guess such a pair for which GCD is 7, and LCM is 91. Which riddle could Simon guess? A: Katy B: Hana C: neither D: both
Hana gave Simon a riddle: guess a pair of numbers whose GCD is 7, and LCM is 90. Katy wanted Simon to guess such a pair for which GCD is 7, and LCM is 91. Which riddle could Simon guess? A: Katy B: Hana C: neither D: both - Dividing
 One always remained when dividing the tangerines into packages of 8 or 10. If there were more than 250 and less than 300, how many were there?
One always remained when dividing the tangerines into packages of 8 or 10. If there were more than 250 and less than 300, how many were there? - Scrapbook
 Jo is making a scrapbook for her best friend's 5th-grade graduation. She used 72 photos with six photos on each page. Jo had to remove two photos on each page to make room for the writing she wanted to include. Write an expression that represents the numb
Jo is making a scrapbook for her best friend's 5th-grade graduation. She used 72 photos with six photos on each page. Jo had to remove two photos on each page to make room for the writing she wanted to include. Write an expression that represents the numb - Happy marriage
 Jan and Marienka have been in a happy marriage for several years. Jan's age is written in the same numbers as Marienka's, only in reverse order. Their ages differ by just a fifth of Marienka's. Jan is older. How old is Jan, and how many is Marienka?
Jan and Marienka have been in a happy marriage for several years. Jan's age is written in the same numbers as Marienka's, only in reverse order. Their ages differ by just a fifth of Marienka's. Jan is older. How old is Jan, and how many is Marienka? - Twenty
 Twenty rabbits are put in 4 cells so that there are a different number of rabbits in each cell containing at least three rabbits. What is the largest possible number of rabbits in one cell?
Twenty rabbits are put in 4 cells so that there are a different number of rabbits in each cell containing at least three rabbits. What is the largest possible number of rabbits in one cell? - Number with ones
 The first digit of the number is 1. If we move this digit to the end, we get three times the higher number. What is the number?
The first digit of the number is 1. If we move this digit to the end, we get three times the higher number. What is the number? - Florist
 The florist has 84 red and 48 white roses. How many bouquets can he make from them if he must use all roses?
The florist has 84 red and 48 white roses. How many bouquets can he make from them if he must use all roses? - Children 82437
 If 3 boys were added to the eighth grade, 50% of the class would be boys. If, on the other hand, 3 girls were added, they would make up 7/12 classes. How many children are there in the class?
If 3 boys were added to the eighth grade, 50% of the class would be boys. If, on the other hand, 3 girls were added, they would make up 7/12 classes. How many children are there in the class? - Received 81440
 At the flower festival, young growers sold cactus plants for CZK 12 and indoor violet plants for CZK 9. They sold a total of 47 pieces of flowers of both types and received CZK 501. How many cacti and how many violets did they sell?
At the flower festival, young growers sold cactus plants for CZK 12 and indoor violet plants for CZK 9. They sold a total of 47 pieces of flowers of both types and received CZK 501. How many cacti and how many violets did they sell? - Arranged 80453
 There are 390 trees arranged in rows in the orchard. How many rows are there if each row has the same number of trees greater than 30 and less than 40?
There are 390 trees arranged in rows in the orchard. How many rows are there if each row has the same number of trees greater than 30 and less than 40? - Different 44621
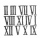 Express the number 68 as this property's sum of two different summands. If you divide a larger sum by a smaller sum, will you receive a result of 3?
Express the number 68 as this property's sum of two different summands. If you divide a larger sum by a smaller sum, will you receive a result of 3? - Athletics 24911
 The sports class is attended by athletes, cyclists, and football players. The number of athletes to cyclists is in the ratio 3:5, football players to cyclists 1:3. How many athletes attend the class if 9 children are involved in athletics?
The sports class is attended by athletes, cyclists, and football players. The number of athletes to cyclists is in the ratio 3:5, football players to cyclists 1:3. How many athletes attend the class if 9 children are involved in athletics? - Regularly 7749
 Three steamers leave the port. The first regularly returns after three months, the second after four, and the third after six months. How long before they meet again in the port?
Three steamers leave the port. The first regularly returns after three months, the second after four, and the third after six months. How long before they meet again in the port? - Shelves 7633
 Juraj had music CDs and DVDs stored on the shelves. There are a total of 64. How many DVDs are on the shelf if there are seven times less than a CD?
Juraj had music CDs and DVDs stored on the shelves. There are a total of 64. How many DVDs are on the shelf if there are seven times less than a CD?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
