Numbers - math word problems - page 304 of 307

Number of problems found: 6127

Rectangular cuboid
The rectangular cuboid has a surface area 4131 cm², and its dimensions are in the ratio 2:4:5. Find the volume of this rectangular cuboid.
Dice coin probability
We roll the dice and then toss the coin as many times as the number that came up on the dice. What is the probability that the coin lands head at least once?
Cube edges length
If we reduce the length of the cube edge by 30%, this reduced cube has an area of 1176 cm². Specify the edge length and volume of the original cube.
Karel grade average
Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one.
Copper winding
Calculate the current flowing through the copper winding at an operating temperature of 70°C Celsius if the winding diameter is 1.128 mm and the coiled length is 40 m. The winding is connected to 8V.
Division residue proof
If n is a natural number that gives a division of 2 or 3 when divided by 5, then n gives a residue of 4 when divided by 5. Prove directly
Number divisibility probability
What is the probability that any two-digit number a) is divisible by five b) is it not divisible by five?
Shooter
The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot?
Logs
The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm?
Two pots
Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot
Aircraft angines
The aircraft's two engines are enough to supply the fuel for five hours of operation. However, one of the engines has malfunctioned and thus consumes one-third more fuel. How long can the plane be in the air before it runs out of fuel? After an hour of ma
ABS, ARG, CONJ, RECIPROCAL
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Transforming cuboid
A cuboid with dimensions 6 cm, 10, and 11 cm is converted into a cube with the same volume. What is its edge length?
Mixture of nuts
We should prepare the mixture of nuts from almonds, peanuts, and nuts cashew ratio of 1:2:3 (respectively). The price of almonds is 150 CZK/kg, the price of peanuts is 140 CZK/kg, and the price of cashew nuts is 180 CZK/kg. The price of the mixture is det
Three-day trip
George went on a moped for a three-day trip. He drove 90 km on the first day, 30 km on the second day, and 60 km on the third day. He always drove at the same average speed and always the whole number of hours. Calculate the average speed if George drove
Which
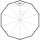Which of the following numbers is the most accurate area of a regular decagon with side s = 2 cm? (A) 9.51 cm² (B) 20 cm² (C) 30.78 cm² (D) 31.84 cm² (E) 32.90 cm²
Spherical cap
From the sphere with a radius of 26 was a truncated spherical cap. Its height is 2. What part of the volume is a spherical cap from the whole sphere?
Alarm clock
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
Cross-section - trapezoid
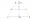The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width.
Probability
A man had 4 coins, some $2, some $1. The coins had a number on one side and a picture on the other. The man flipped them, and the sum of the numbers on the tops of the coins was 1. The probability of this happening was 1/8. What was the probability that i

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.