Prism + diagonal - practice problems
Number of problems found: 67
- Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Four sided prism
 Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane.
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - Rhombus base
 Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. Prism height is twice the base edge length.
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. Prism height is twice the base edge length. - Quadrilateral prism
 The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume.
The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume.
- Trapezoidal prism
 Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Support colum
 Calculate the support column's volume and surface, which is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. Column height is 1. 5m.
Calculate the support column's volume and surface, which is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. Column height is 1. 5m. - Calculate 23411
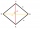 The prism with a diamond base has one base diagonal of 20 cm and a base edge of 26 cm. The edge of the base is 2:3 to the height of the prism. Calculate the volume of the prism.
The prism with a diamond base has one base diagonal of 20 cm and a base edge of 26 cm. The edge of the base is 2:3 to the height of the prism. Calculate the volume of the prism. - Quadrilateral 47493
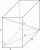 A regular quadrilateral prism ABCDEFGH has a base edge A B 8 cm long and 6 cm high. Point M is the center of the edge AE. Determine the distance of point M from the BDH plane.
A regular quadrilateral prism ABCDEFGH has a base edge A B 8 cm long and 6 cm high. Point M is the center of the edge AE. Determine the distance of point M from the BDH plane. - Diamond base
 The prism with a diamond base has 24 cm and 20 cm long base diagonals. Calculate the height of a prism with a volume of 9.6 dm³ (cubic decimetres)
The prism with a diamond base has 24 cm and 20 cm long base diagonals. Calculate the height of a prism with a volume of 9.6 dm³ (cubic decimetres)
- Prism 4 sides
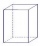 The prism has a square base with a side length of 3 cm. The diagonal of the sidewall of the prism/BG/is 5 cm. Calculate the surface of this prism in cm square and the volume in liters
The prism has a square base with a side length of 3 cm. The diagonal of the sidewall of the prism/BG/is 5 cm. Calculate the surface of this prism in cm square and the volume in liters - Total area
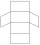 Calculate the total area (surface and bases) of a prism whose base is a rhombus which diagonals of 12cm and 18cm and prism height are 10 cm.
Calculate the total area (surface and bases) of a prism whose base is a rhombus which diagonals of 12cm and 18cm and prism height are 10 cm. - Quadrilateral 8304
 The base of the quadrilateral prism is a diamond with diagonals of 7 and 9 cm. The height of the prism is 22 cm. What is the area?
The base of the quadrilateral prism is a diamond with diagonals of 7 and 9 cm. The height of the prism is 22 cm. What is the area? - Prism diagonal
 The body diagonal of a regular square prism has an angle of 60 degrees with the base, and the edge length is 10 cm. What is the volume of the prism?
The body diagonal of a regular square prism has an angle of 60 degrees with the base, and the edge length is 10 cm. What is the volume of the prism? - Calculate 2558
 Calculate the size of the solid diagonals of a prism with a rhombus base if the sizes of the base diagonals are 16 cm and 20 cm and the height of the prism is 32 cm. Calculate the size of the base edge.
Calculate the size of the solid diagonals of a prism with a rhombus base if the sizes of the base diagonals are 16 cm and 20 cm and the height of the prism is 32 cm. Calculate the size of the base edge.
- Logs
 The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm?
The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm? - Quadrilateral 83307
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Regular hexagonal prism
 Calculate the volume of a regular hexagonal prism whose body diagonals are 24cm and 25cm long.
Calculate the volume of a regular hexagonal prism whose body diagonals are 24cm and 25cm long. - Must-have 7893
 If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter?
If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter? - Calculate 14153
 The base of the vertical prism is a rhombus with diagonals of 24cm and 10cm. Suppose the shell content is 52% of the total surface area of the prism. Calculate its surface.
The base of the vertical prism is a rhombus with diagonals of 24cm and 10cm. Suppose the shell content is 52% of the total surface area of the prism. Calculate its surface.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
