Pythagorean theorem - practice problems - page 5 of 73
Number of problems found: 1449
- Calculate 2577
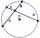 Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm.
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Isosceles triangle
 Find the area of an isosceles triangle whose leg is twice the base, b=1
Find the area of an isosceles triangle whose leg is twice the base, b=1 - Equilateral triangle
 Find the area of an equilateral triangle with a side of 15 cm.
Find the area of an equilateral triangle with a side of 15 cm. - Area of a rectangle
 Calculate a rectangle area with a diagonal of u = 12.5cm and a width of b = 3.5cm. Use the Pythagorean theorem.
Calculate a rectangle area with a diagonal of u = 12.5cm and a width of b = 3.5cm. Use the Pythagorean theorem. - Square
 Calculate the square's perimeter and area with a diagonal length of 30 cm.
Calculate the square's perimeter and area with a diagonal length of 30 cm. - Calculate hexagon
 Calculate the area of a regular hexagon with side a = 2cm.
Calculate the area of a regular hexagon with side a = 2cm. - Square2
 The side of the square is a = 5.6 cm. How long is its diagonal?
The side of the square is a = 5.6 cm. How long is its diagonal? - Calculate 10691
 Calculate the length of the side of a square whose diagonal has a length of 10 m.
Calculate the length of the side of a square whose diagonal has a length of 10 m. - Supported 6172
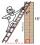 The ladder is 1.4 m from the wall and touches 3 m high. How long is the ladder?
The ladder is 1.4 m from the wall and touches 3 m high. How long is the ladder? - Isosceles triangle
 The given is an isosceles triangle with a base of 24dm and an arm of 15dm. Calculate the height of the triangle.
The given is an isosceles triangle with a base of 24dm and an arm of 15dm. Calculate the height of the triangle. - Tangent of an angle
 Suppose the tangent of an angle of a right-angled triangle is 0.8. Then its longest side is:
Suppose the tangent of an angle of a right-angled triangle is 0.8. Then its longest side is: - Broken tree
 The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Diagonal - simple
 Calculate the length of the diagonal of a rectangle with dimensions 5 cm and 12 cm.
Calculate the length of the diagonal of a rectangle with dimensions 5 cm and 12 cm. - Equilateral triangle v2
 An equilateral triangle has a perimeter 36 dm. What is its area?
An equilateral triangle has a perimeter 36 dm. What is its area? - OPT
 What is the perimeter of a right triangle with the legs 11 cm and 24 cm long?
What is the perimeter of a right triangle with the legs 11 cm and 24 cm long? - Circle chord
 Determine the circle's radius in which the chord 15 cm away from the center is 21 cm longer than the circle's radius.
Determine the circle's radius in which the chord 15 cm away from the center is 21 cm longer than the circle's radius. - Goniometric form
 Determine the goniometric form of a complex number z = √ 110 +4 i.
Determine the goniometric form of a complex number z = √ 110 +4 i. - Base
 Compute the base of an isosceles triangle, with the arm a=10 cm and a height above the base h=7 cm.
Compute the base of an isosceles triangle, with the arm a=10 cm and a height above the base h=7 cm. - Bridge
 The bridge arc has a span of 159 m and a height of 14 m. Calculate the radius of the circle arc of this bridge.
The bridge arc has a span of 159 m and a height of 14 m. Calculate the radius of the circle arc of this bridge. - Height UT
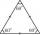 How long is the height in the equilateral triangle with a side f = 31?
How long is the height in the equilateral triangle with a side f = 31?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
