Similarity of triangles - practice problems - page 2 of 8
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 160
- Determine 80754
 The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA.
The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA. - Right-angled 80745
 The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST.
The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST. - Similarity 80742
 Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm.
Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm. - Calculate 80741
 In the camp, the children made a mock-up of the campsite. In its center was a maple, which had a height of 28 cm on the model. Calculate the height of the maple in the campsite if, in the morning, it casts a shadow 14 m long and its model has a shadow 49
In the camp, the children made a mock-up of the campsite. In its center was a maple, which had a height of 28 cm on the model. Calculate the height of the maple in the campsite if, in the morning, it casts a shadow 14 m long and its model has a shadow 49 - Nicolette
 Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel
Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Figure 2
 Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B?
Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B? - Karim
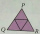 Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your
Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - Shadow 73354
 How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long? - Shadows
 At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow? - Determine 70834
 At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney.
At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney. - Triangle 69144
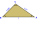 The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle?
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle? - Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Isosceles 67744
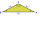 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Calculate 64444
 The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden.
The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden. - Circumference 64104
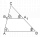 The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '.
The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pentagon
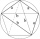 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Calculate
 Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
