Solid geometry, stereometry - page 85 of 121
Number of problems found: 2409
- Aluminum cylinder
 The aluminum cylinder weighs 1400 g and is 26 cm high. Its density is 2700 kg/m³. Calculate the base area of the cylinder and express the result in cm².
The aluminum cylinder weighs 1400 g and is 26 cm high. Its density is 2700 kg/m³. Calculate the base area of the cylinder and express the result in cm². - Triangular prism
 The curved part of the rotating cylinder is four times larger than the area of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm.
The curved part of the rotating cylinder is four times larger than the area of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm. - Equilateral cylinder
 The equilateral cylinder (height = base diameter; h = 2r) has a V = 178 cm³ volume. Calculate the surface area of the cylinder.
The equilateral cylinder (height = base diameter; h = 2r) has a V = 178 cm³ volume. Calculate the surface area of the cylinder. - Decimeters 83242
 The axial section of the cylinder is a square with an area of 56.25 cm². Calculate its surface area and volume. Express the result in square decimeters and cubic decimeters and round to hundredths.
The axial section of the cylinder is a square with an area of 56.25 cm². Calculate its surface area and volume. Express the result in square decimeters and cubic decimeters and round to hundredths. - Spherical 81527
 Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume?
Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume? - Calculate 70634
 The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters.
The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters. - Cube diagonal
 Calculate the length of the body diagonal in a cube of 15 cm.
Calculate the length of the body diagonal in a cube of 15 cm. - Hexagon, hexa S, V
 What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base?
What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base? - Box
 A paper box is in the shape of a cube. 2,400 cm² of paper was used to make it. Bends for gluing the walls are not included. Calculate the volume of the box.
A paper box is in the shape of a cube. 2,400 cm² of paper was used to make it. Bends for gluing the walls are not included. Calculate the volume of the box. - Cuboid's diagonal
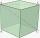 The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid?
The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid? - Regular square prism
 The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism.
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - A plane vs. sphere
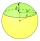 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - Cube in a sphere
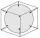 The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube.
The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube. - Cuboid
 Cuboid with edge a=6 cm and space diagonal u=31 cm has volume V=900 cm³. Calculate the length of the other edges.
Cuboid with edge a=6 cm and space diagonal u=31 cm has volume V=900 cm³. Calculate the length of the other edges. - Calculate 30971
 Calculate the cone's surface and volume if its base diameter is 1 dm and the side length is 13 cm.
Calculate the cone's surface and volume if its base diameter is 1 dm and the side length is 13 cm. - Dimensions 20553
 The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume.
The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume. - Quadrilateral 16603
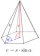 Calculate the volume of a regular quadrilateral pyramid, which has the size of the base edge a = 8 cm and the length of the side edge h = 9 cm.
Calculate the volume of a regular quadrilateral pyramid, which has the size of the base edge a = 8 cm and the length of the side edge h = 9 cm. - 4B - truncated pyramid
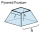 Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Spherical segment
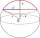 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Perpendicular prism network
 Find the volume and surface of a triangular prism with the base of a right triangle, the network of which is 4 cm 3 cm (perpendiculars) and nine centimeters (height of the prism).
Find the volume and surface of a triangular prism with the base of a right triangle, the network of which is 4 cm 3 cm (perpendiculars) and nine centimeters (height of the prism).
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
