Solid geometry, stereometry - page 120 of 121
Number of problems found: 2409
- Pyramid
 The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side.
The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side. - Pentagonal prism
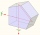 The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism.
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism. - Angle of cone
 The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone. - The hemisphere
 The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees?
The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees? - Earth parallel
 Earth's radius is 6377 km long. Calculate the length parallel to latitude 75°.
Earth's radius is 6377 km long. Calculate the length parallel to latitude 75°. - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Pentagonal pyramid
 Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees.
Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees. - House volume
 V = 35 m α = 55° β = 15° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =?
V = 35 m α = 55° β = 15° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =? - Cone slope
 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - Heptagonal pyramid
 A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Cube - angles
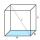 Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base.
Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base. - Box
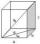 Calculate the angle between box base 5 x 10 and body diagonal length 13.
Calculate the angle between box base 5 x 10 and body diagonal length 13. - House roof
 The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof?
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof? - Earth's circumference
 Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes.
Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes. - Cuboid diagonal
 Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees.
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees. - Pilot
 How high can the airplane's pilot see 0.001 of Earth's surface?
How high can the airplane's pilot see 0.001 of Earth's surface? - Sphere in cone
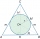 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Angle of the body diagonals
 Using the vector dot product calculate the angle of the body diagonals of the cube.
Using the vector dot product calculate the angle of the body diagonals of the cube. - Big Earth
 What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - Tropical, mild and arctic
 How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'.
How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
