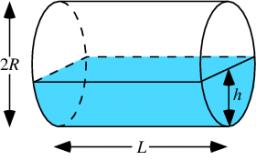
Cylinder horizontally
The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder?
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetrybasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cylindrical bucket
The cylindrical bucket was filled 2/3 with water. You know that the diameter of the bottom is 25 cm, and the water reaches a height of 24 cm. What is the maximum amount of water that can be poured into the bucket? - Pool water
The children's pool has the shape of a cylinder with a bottom diameter of 6 m and a height of 60 cm. The water reaches one decimeter below the top of the pool. How many hectoliters of water is in the pool? - Hectoliters
If a garden barrel with a 90 cm diameter and a height of 1.3 m is filled to 80% of its capacity, how many hectoliters of water is in it? - Cylinder container
If the cylinder-shaped container is filled with water to a height of 5 dm, it contains 62.8 hectoliters of water. Calculate the diameter of the bottom of the container. Use the value π = 3.14. - Cylindrical tank
9.6 hl of water is poured into a cylindrical tank with a bottom diameter of 1.2 m. What height in centimeters does the water reach? - Water overflow
A rectangular container has a length of 30 cm, a width of 20 cm, and a height of 24 cm. It is filled with water to a depth of 15 cm. Some water overflows when an additional 6.5 liters of water is poured into the container. How many liters of water overflo - Tank water hectoliters
How many hectoliters of water are in a cylindrical water tank with a base diameter of 3 meters and a depth of 60 cm?
