Solid geometry, stereometry - page 94 of 121
Number of problems found: 2404
- Increase 46473
He enlarges the side of the 8 cm long cube by 20%. How much will its volume increase compare to the original cube? - Radius of a sphere
We turned a sphere with the largest possible radius from a cube with an edge length of 8 cm. Calculate the volume of the cube, the ball, and the percentage of waste when turning. - Hectoliters 3382
The block tank held 288 hectoliters of water. The bottom dimensions are 12m and 6m, and the depth is 2m. What percent of the tank volume does the water occupy? - Cylindrical container
An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container. - Completely 67674
A) Can the maximum number of sugar cubes with a volume of 3375 cubic mm fit in a new cube-shaped sugar bowl with internal dimensions of 12 cm, 6 cm, and 3 cm? B) Mom poured sugar cubes into the new sugar bowl, filling it completely. She estimated that the - Wrapping 36303
How much will we pay for wrapping 5 boxes in the shape of a cube with a side length of 80 cm if we count on a margin of 35% for folds? The price for 1 square meter of paper is €2.55. You can only buy whole square meters. - Forest area
The Earth's surface is approximately 510,000,000 km². The forest area is about 38,000,000 km². Write a fraction in the basic form. What part of the Earth's surface is formed by the forest? - Cube, cuboid, and sphere
Volumes of a cube and a cuboid are in a ratio of 3:2. Volumes of a sphere and cuboid are in a ratio of 1:3. At what rate are the volumes of a cube, cuboid, and sphere? - Parameters 28521
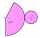The basic parameters of the rotating cone are: Base radius 5 cm The cone height is 12 cm, and the cone side is 13 cm. Calculate: a/volume of the cone b/cone surface - Dimensions of an aquarium
The large aquarium is shaped like a cuboid and has dimensions in the ratio 5: 7: 4. The sum of the lengths of all edges is 96 dm. How many liters of water will be in the aquarium if it is filled to four-fifths? - Tanks
The fire tank is cuboid in shape, with a rectangular floor measuring 13.3 m × 14.7 m. The water depth is 1.9 m. Water was pumped from the tank into barrels with a capacity of 5 hl. How many barrels would have been used if the water level in the tank - Cylinder melted into cuboid
A circular cylinder has an area of cross-section of 56 cm², and the height is 10cm. The cylinder is melted into a cuboid with a base area of 16 cm². What is the height of the cuboid? - Surface of a cube
The cube's edge, the volume of which is 58.3% of its surface, is: a) 3.5cm b) 4.5cm c) 2.5cm d) 1.5cm - Carefully 12791
Spruce logs with a diameter of 270 mm and a length of 4 m are carefully loaded onto a wagon with a bed width of 2,700 mm and stacked in 9 layers. How much does such a load of spruce wood weigh if its density is 700 kg/m³? - Cylinder's 83130
Calculate the cylinder's volume if you know that the ratio of the cylinder's height to the base's radius is 3:2 and the height is 15 dm. - Cube-shaped 81931
A ball with a diameter of 10 cm is in a cube-shaped box with an edge of 10 cm. What percentage of the box does the ball fill? - How many 9
How much percent volume remains of a sphere if the diameter decrease 3×? - Volume ratio
Calculate the volume ratio of balls circumscribed (diameter r) and inscribed (diameter ϱ) into an equilateral rotating cone. - Sphere radius
We reduce the radius of the sphere by 1/3 of the original radius. How much percent does the volume and surface of the sphere change? - Cube surface area
The cube's surface was originally 216 centimeters square. It has shrunk from 216 to 54 centimeters square. Calculate the percent change in the edge of the cube.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
