Square root - math word problems - page 32 of 69

Number of problems found: 1376

Cube surfce2volume
Calculate the volume of the cube if its surface is 150 cm².
Motorcyclist and a car
The passenger car left at 7:00 and was heading east at a speed of 60 km/h. A motorcyclist left the same place and headed north at 40 km/h. What will be their air distance at ten o'clock?
Horizontal 26131
What height difference does the 2.5 km long ski lift overcome when the horizontal distance of the entry and exit station is 1200 meters?
Cuboid to cube
A cuboid with dimensions of 9 cm, 6 cm, and 4 cm has the same volume as a cube. Calculate the surface of this cube.
The cube
The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume.
Surface of pyramid
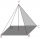A regular quadrilateral pyramid has the height of the sidewall equal to the length of the edge of the base. The area of the sidewall is 32 cm². What is the surface of the pyramid?
Height of pyramid
The pyramid ABCDV has edge lengths: AB = 4, AV = 7. What is its height?
Perimeter 24701
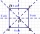The sales stand floor plan consists of squares and has an area of 48 m². What is the perimeter of these booths? a. 34 m b. 36 m c. 40 m d. 44 m
Two parallel chords
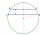In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long.
Percentage increase
What is the annual percentage increase in the city when the population has tripled in 20 years?
Magnified cube
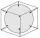If the lengths of the cube's edges are extended by 5 cm, its volume will increase by 485 cm³. Determine the surface of both the original and the magnified cube.
Millimeter 24231
Calculate the length of the wall diagonal of a cube with a volume of 7.40 square meters. Express the result to the nearest millimeter.
Body diagonal
Calculate the surface area, volume, and length of the body diagonal of a cube with an edge length of 4 dm.
Quadrilateral prism
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?
Triangular 24091
A regular triangular prism with a base edge of 35 cm has a volume of 22.28 l. Calculate its height.
Centimeter 23781
Calculate the diameter of a cylinder 7.5 dm high with a volume of 0.6 hl. Express the result to the nearest centimeter.
Quadrilateral 23701
We know a regular quadrilateral pyramid's base diagonal length of u = 4 cm. The height of the pyramid is v = 5cm. Calculate the size of the side edge and the base edge of the pyramid.
Difference - altitude
The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter?
Concentric circles and chord
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord?
Dimensions 22991
What are the dimensions of a square with an area of 49dm square?

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.