Square practice problems - page 116 of 150
Number of problems found: 3000
- Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Base diameter
 Calculate the volume and surface of a cone whose base diameter is 6 cm and height is 0.9 dm.
Calculate the volume and surface of a cone whose base diameter is 6 cm and height is 0.9 dm. - Quadrangular pyramid
 The decorative object has a quadrangular pyramid shape. Its base edge is 0.7 dm, and its side edge is 1.4 dm long. Calculate its height.
The decorative object has a quadrangular pyramid shape. Its base edge is 0.7 dm, and its side edge is 1.4 dm long. Calculate its height. - Calculate pyramid
 Calculate the volume of the pyramid, whose base edge a = 8 cm and the sidewall makes an angle α = 60° with the square base.
Calculate the volume of the pyramid, whose base edge a = 8 cm and the sidewall makes an angle α = 60° with the square base. - Prism 4 sides
 The prism has a square base with a side length of 3 cm. The diagonal of the sidewall of the prism (BG) is 5 cm. Calculate the surface of this prism in cm square and the volume in liters.
The prism has a square base with a side length of 3 cm. The diagonal of the sidewall of the prism (BG) is 5 cm. Calculate the surface of this prism in cm square and the volume in liters. - Above Earth
 To what height must a boy be raised above the earth to see one-fifth of its surface?
To what height must a boy be raised above the earth to see one-fifth of its surface? - Lamp cone
 Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm.
Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm. - Snow wall
 The boys want to build a defensive wall out of the snow for the ballpark. They want it to be 5 meters long and 1.5 meters high. They can make and transfer 50 cm cubes from snow. How many such cubes must he make to build his wall?
The boys want to build a defensive wall out of the snow for the ballpark. They want it to be 5 meters long and 1.5 meters high. They can make and transfer 50 cm cubes from snow. How many such cubes must he make to build his wall? - Cone surface radius
 The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface.
The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface. - Bar volume triangle
 The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume
The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume - Cone volume surface
 A right triangle with perpendiculars a = 3 cm and b = 4 cm rotates around a longer perpendicular. Calculate the volume and surface area of the resulting cone.
A right triangle with perpendiculars a = 3 cm and b = 4 cm rotates around a longer perpendicular. Calculate the volume and surface area of the resulting cone. - Trapezoid height angle
 In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Cube small diagonal
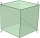 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Cone surface volume
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Cube diagonal calculation
 Calculate the length of the wall diagonal of a cube with a volume of 7.40 square meters. Express the result to the nearest millimeter.
Calculate the length of the wall diagonal of a cube with a volume of 7.40 square meters. Express the result to the nearest millimeter. - Cube diagonals
 The cube has a wall area of 81 cm square. Calculate the length of its edge, wall, and body diagonal.
The cube has a wall area of 81 cm square. Calculate the length of its edge, wall, and body diagonal. - Axial section
 The axial section of the cone is an equilateral triangle with an area 208 km². Calculate the volume of the cone.
The axial section of the cone is an equilateral triangle with an area 208 km². Calculate the volume of the cone. - Cube - angles
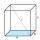 Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base.
Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base. - Triangular prism volume
 Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm.
Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm. - Block wall diagonal
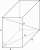 A block with dimensions a = 15cm b = 5cm and a block height c = 8cm. Calculate the length of the wall diagonal in the base.
A block with dimensions a = 15cm b = 5cm and a block height c = 8cm. Calculate the length of the wall diagonal in the base.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
