Trapezoid + quadrilateral - practice problems
Number of problems found: 19
- Trapezoidal prism
 Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Quadrilateral-trapezoid 3172
 We cut two triangles from the rectangular plate so that the resulting quadrilateral-trapezoid with the same arm lengths has an area of 32 cm², and one of its bases is twice as long as the other. What is the area of the two triangles that make up the waste
We cut two triangles from the rectangular plate so that the resulting quadrilateral-trapezoid with the same arm lengths has an area of 32 cm², and one of its bases is twice as long as the other. What is the area of the two triangles that make up the waste - Centimeters 6604
 A four-sided prism has a volume of 648 cubic centimeters. The trapezoid that is its base has the dimensions a is equal to 10 centimeters, c is equal to eight centimeters, and height v is equal to 6 centimeters. Calculate the height of the prism.
A four-sided prism has a volume of 648 cubic centimeters. The trapezoid that is its base has the dimensions a is equal to 10 centimeters, c is equal to eight centimeters, and height v is equal to 6 centimeters. Calculate the height of the prism. - Quadrangular prism
 The quadrangular prism has a volume of 648 cm³. Trapezoid which is its base has the dimensions bases: a = 10 cm, c = 5 and height v = 6 cm. What is the height of the prism?
The quadrangular prism has a volume of 648 cm³. Trapezoid which is its base has the dimensions bases: a = 10 cm, c = 5 and height v = 6 cm. What is the height of the prism?
- Determine
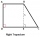 Determine which type of quadrilateral ABCD is and find its perimeter if you know the coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /.
Determine which type of quadrilateral ABCD is and find its perimeter if you know the coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /. - Trapezoidal base
 Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, height of trapezium v = 3.7 cm and the height of the prism h = 5 cm.
Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, height of trapezium v = 3.7 cm and the height of the prism h = 5 cm. - Square
 Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm².
Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm². - Quadrilateral 80729
 Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD.
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Truncated pyramid
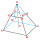 Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
- The base
 The base of the quadrilateral prism is a trapezoid with an area of 75 cm square. The prism is 6 cm high. Find the volume of the prism.
The base of the quadrilateral prism is a trapezoid with an area of 75 cm square. The prism is 6 cm high. Find the volume of the prism. - Perpendicular 81381
 Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m.
Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m. - Trapezoid
 Are diagonals in a rectangular trapezoid perpendicular and bisect the angles?
Are diagonals in a rectangular trapezoid perpendicular and bisect the angles? - Quadrilateral 24161
 Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated? - Parallelogram
 Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A.
Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A.
- Quadrilateral 7583
 For the sizes of the interior angles of the quadrilateral ABCD, the following applies: the angle alpha is 26° greater than the angle beta, twice the angle Beta is 5° less than the angle gamma, and the angle gamma is 36° greater than the angle delta. Deter
For the sizes of the interior angles of the quadrilateral ABCD, the following applies: the angle alpha is 26° greater than the angle beta, twice the angle Beta is 5° less than the angle gamma, and the angle gamma is 36° greater than the angle delta. Deter - Truncated pyramid
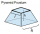 The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Inaccessible 69794
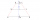 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Quadrilateral 2
 Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles.
Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles. - 4-gon
 Is it true that a 4-gon whose two sides are parallel and the other two have equal length is a parallelogram?
Is it true that a 4-gon whose two sides are parallel and the other two have equal length is a parallelogram?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Trapezoid practice problems. Quadrilateral practice problems.
