The volume of cone problems - page 6 of 9
Number of problems found: 164
- A concrete pedestal
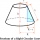A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume. - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Right circular cone
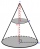The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - Lateral surface area
The ratio of the area of the base of the rotary cone to its lateral surface area is 3:5. Calculate the surface and volume of the cone if its height v = 4 cm. - Castle model The castle model has a cone-shaped roof. The cone side is 45 cm long, and the base radius is 27 cm. a) What is the roof volume? b) How much dm² of wallpaper is used to glue the roof, i.e., the cone shell? c) What is the roof's weight if it is made of wood
- Without 8260
The ice cream sundae glass has a cone shape. Its height without legs is 9 cm, and its radius is 5 cm. Šimon bought eight scoops of ice cream, which all melted in the sun. One scoop of ice cream has a volume of 32 cm³. How many cm³ of melted ice cream will - Children's 8246
We prepare a pile of sand in the shape of a cone with a height of 1 m and a diameter of 1.6 m. We prepare it for the children's sandpit. What volume of sand does this pile occupy?
- The diagram 2
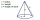The diagram shows a cone with a slant height of 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate to correct three significant figures: *Base Radius *Height *Volume of the cone - Cone-shaped 8170
How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer. - Pile of sand
A large pile of sand has been dumped into a conical pile in a warehouse. The slant height of the pile is 20 feet. The diameter of the base of the sandpile is 31 feet. Find the volume of the pile of sand. - Rotating 7947
In the rotating cone = 100π S rotating cone = 90π v =? r =? - Pyramid 7903
How does the volume of a pyramid change if we triple its height? - Confectionery 7318
The confectioner needs to carve a cone-shaped decoration from a ball-shaped confectionery mass with a radius of 25 cm. Find the radius of the base of the ornament a (and the height h). He uses as much material as possible is used to make the ornament. - Slant height
Find the cone's volume. The cone's slant height is 5cm, and the radius of its base is 3cm. - Volcano
The volcano's crater is approximately in the shape of a cone with a base of 3.1416 square miles. The crater's depth is 1500 ft. How many cubic yards of earth would be required to fill this cavity?
- Rotating cone
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times - Inscribed 6155
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies. - Volume of cone
Find the volume of a right circular cone-shaped building with a height of 9 m and a radius base of 7 m. - Calculate 5789
Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm. - Conical area
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Tip: Our volume units converter will help you convert volume units. Volume - practice problems. Cone practice problems.
