The volume of cone problems - page 8 of 9
Number of problems found: 164
- Sphere
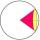Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere. - Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions. - Cone
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - Sphere and cone
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Cross-sections of a cone
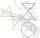Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Truncated cone
Calculate the height of the rotating truncated cone with volume V = 1471 cm³ and a base radii r1 = 6.1 cm and r2 = 7.9 cm. - Ice cream in cone
The ice cream cone with a diameter of 5.4 cm is 1.2 dl of ice cream. Calculate the depth of the cone.
- Rotary cone
The volume of the rotation of the cone is 733 cm³. The angle between the side of the cone and the base angle is 75°. Calculate the lateral surface area of this cone. - Cut and cone
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Cone
Calculate the volume and surface area of the cone with a diameter of the base d=16 cm and the side of the cone with the base has angle 37°12'. - Rotary cone
A rotary cone whose height is equal to the circumference of the base has a volume 229 cm³. Calculate the radius of the base circle and the height of the cone. - Cone
If the segment of the line y = -3x +4 that lies in the first quadrant is rotated about the y-axis, a cone is formed. What is the volume of the cone? - 2x cone
Circular cone height 36 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Cone
The circular cone of height 14 cm and volume 4396 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Cone A2V
The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone.
- Axial section
The axial section of the cone is an equilateral triangle with an area 208 km². Calculate the volume of the cone. - Rotation
The right triangle with legs 11 cm and 18 cm rotates around the longer leg. Calculate the volume and surface area of the formed cone. - Cone
The circular cone has height h = 15 dm and base radius r = 2 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume. - Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm. - Cone and cube
About what percentage has cone with base radius r larger volume than a same high cube with square base with edge length r?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Tip: Our volume units converter will help you convert volume units. Volume - practice problems. Cone practice problems.
