Fraction calculator
This calculator divides fractions. The first step makes the reciprocal value of the second fraction - exchange numerator and denominator of 2nd fraction. Then multiply both numerators and place the result over the product of both denominators. Then simplify the result to the lowest terms or a mixed number.
The result:
1/3 / 2/5 = 5/6 ≅ 0.8333333
The spelled result in words is five sixths.How do we solve fractions step by step?
- Divide: 1/3 : 2/5 = 1/3 · 5/2 = 1 · 5/3 · 2 = 5/6
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 2/5 is 5/2) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words - one third divided by two fifths is five sixths.
Rules for expressions with fractions:
Fractions - use a forward slash to divide the numerator by the denominator, i.e., for five-hundredths, enter 5/100. If you use mixed numbers, leave a space between the whole and fraction parts.Mixed numerals (mixed numbers or fractions) keep one space between the integer and
fraction and use a forward slash to input fractions i.e., 1 2/3 . An example of a negative mixed fraction: -5 1/2.
Because slash is both sign for fraction line and division, use a colon (:) as the operator of division fractions i.e., 1/2 : 1/3.
Decimals (decimal numbers) enter with a decimal point . and they are automatically converted to fractions - i.e. 1.45.
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| - | minus sign | subtraction | 1 1/2 - 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 |
| : | colon | complex fraction | 1/2 : 1/3 |
| ^ | caret | exponentiation / power | 1/4^3 |
| () | parentheses | calculate expression inside first | -3/5 - (-1/4) |
Examples:
• adding fractions: 2/4 + 3/4• subtracting fractions: 2/3 - 1/2
• multiplying fractions: 7/8 * 3/9
• dividing Fractions: 1/2 : 3/4
• reciprocal of a fraction: 1 : 3/4
• square of a fraction: 2/3^2
• cube of a fraction: 2/3^3
• exponentiation of a fraction: 1/2^4
• fractional exponents: 16 ^ 1/2
• adding fractions and mixed numbers: 8/5 + 6 2/7
• dividing integer and fraction: 5 ÷ 1/2
• complex fractions: 5/8 : 2 2/3
• decimal to fraction: 0.625
• Fraction to Decimal: 1/4
• Fraction to Percent: 1/8 %
• comparing fractions: 1/4 2/3
• multiplying a fraction by a whole number: 6 * 3/4
• square root of a fraction: sqrt(1/16)
• reducing or simplifying the fraction (simplification) : 4/22 - dividing the numerator and denominator of a fraction by the same non-zero number - equivalent fraction
• expression with brackets: 1/3 * (1/2 - 3 3/8)
• compound fraction: 3/4 of 5/7
• fractions multiple: 2/3 of 3/5
• divide to find the quotient: 3/5 ÷ 2/3
The calculator follows well-known rules for the order of operations. The most common mnemonics for remembering this order of operations are:
PEMDAS - Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
BEDMAS - Brackets, Exponents, Division, Multiplication, Addition, Subtraction
BODMAS - Brackets, Of or Order, Division, Multiplication, Addition, Subtraction.
GEMDAS - Grouping Symbols - brackets (){}, Exponents, Multiplication, Division, Addition, Subtraction.
MDAS - Multiplication and Division have the same precedence over Addition and Subtraction. The MDAS rule is the order of operations part of the PEMDAS rule.
Be careful; always do multiplication and division before addition and subtraction. Some operators (+ and -) and (* and /) have the same priority and must be evaluated from left to right.
Fractions in word problems:
- David 4
 David made 4/3 of a quart of fruit juice. Each mug he has holds 1/3 of a quart. How many mugs will David be able to fill?
David made 4/3 of a quart of fruit juice. Each mug he has holds 1/3 of a quart. How many mugs will David be able to fill? - Divide 42
 Divide. Write your answer in the lowest terms as a proper or improper fraction. (8/25)÷(-4/5)
Divide. Write your answer in the lowest terms as a proper or improper fraction. (8/25)÷(-4/5) - Divide mixed numbers
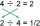 Divide the following fractions and reduce your answers to its simplest form if possible: 1. 2 3/4 ÷ 3 1/12 2. 3 2/3 ÷ 4 1/2 3. 5 3/7 ÷ 2 3/9 4. 6 2/3 ÷ 1 1/5
Divide the following fractions and reduce your answers to its simplest form if possible: 1. 2 3/4 ÷ 3 1/12 2. 3 2/3 ÷ 4 1/2 3. 5 3/7 ÷ 2 3/9 4. 6 2/3 ÷ 1 1/5 - How many 34
 How many groups of 34 are in 114? Write your answer as a mixed number in simplest form.
How many groups of 34 are in 114? Write your answer as a mixed number in simplest form.
- Julian 2
 Julian and two of his friends will share 1/4 of a pizza. How much will each person get?
Julian and two of his friends will share 1/4 of a pizza. How much will each person get? - Convert 6
 Convert to a decimal 15/100.
Convert to a decimal 15/100. - Solve 21
 Solve the following problem and write the answer as a mixed number in the lowest terms: 8/11 ÷ 4/9.
Solve the following problem and write the answer as a mixed number in the lowest terms: 8/11 ÷ 4/9. - One half 2
 One-half pizza will be divided among three pupils. Each pupil receives 1/6. Is it true or false?
One-half pizza will be divided among three pupils. Each pupil receives 1/6. Is it true or false? - A reciprocal
 What is the reciprocal for 4/3? ("RECIPROCAL" is the math word for when we FLIP a fraction...Example: the reciprocal of 3/4 is 4/3.)
What is the reciprocal for 4/3? ("RECIPROCAL" is the math word for when we FLIP a fraction...Example: the reciprocal of 3/4 is 4/3.)
- Pizza 5
 You have 2/4 of a pizza, and you want to share it equally between 2 people. How much pizza does each person get?
You have 2/4 of a pizza, and you want to share it equally between 2 people. How much pizza does each person get? - A lawn
 Sean and his sister, Betty, equally mowed 8/9th of the total area of a lawn. What fraction of the total area did each of them mow?
Sean and his sister, Betty, equally mowed 8/9th of the total area of a lawn. What fraction of the total area did each of them mow? - Fraction 77774
 Express the value of the fraction 25/12 as a decimal number.
Express the value of the fraction 25/12 as a decimal number. - Julian 3
 Julian had 7 cookies and gave half of them to a friend. How many cookies did his friend get?
Julian had 7 cookies and gave half of them to a friend. How many cookies did his friend get? - There 20
 There is 1/2 of a pizza left for four friends to share. What fraction of a pizza will each friend get to eat?
There is 1/2 of a pizza left for four friends to share. What fraction of a pizza will each friend get to eat?
more math problems »