Z9–I–1
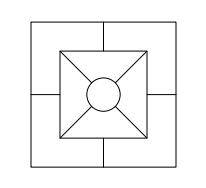
All nine fields of given shape are to be filled with natural numbers so that:
• each of the numbers 2, 4, 6, and 8 is used at least once,
• four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square,
• in the circle is the sum of the numbers of adjacent cells of the inner square.
Find out the smallest and the largest number that can be written in a circle.
• each of the numbers 2, 4, 6, and 8 is used at least once,
• four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square,
• in the circle is the sum of the numbers of adjacent cells of the inner square.
Find out the smallest and the largest number that can be written in a circle.
Final Answer:
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsnumbersthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Twenty
 Twenty rabbits are put in 4 cells so that there are a different number of rabbits in each cell containing at least three rabbits. What is the largest possible number of rabbits in one cell?
Twenty rabbits are put in 4 cells so that there are a different number of rabbits in each cell containing at least three rabbits. What is the largest possible number of rabbits in one cell? - Determine 5893
 Determine the largest integer n for which the square table n×n can be filled with natural numbers from 1 to n² (n squared) so that at least one square power of the integer is written in each of its 3×3 square parts.
Determine the largest integer n for which the square table n×n can be filled with natural numbers from 1 to n² (n squared) so that at least one square power of the integer is written in each of its 3×3 square parts. - Difference 68664
 The digits 1, 2, 4, and 8 form two four-digit numbers so that all 4 digits are used in the notation of each number. Calculate the difference between such largest even number and smallest odd number (in that order).
The digits 1, 2, 4, and 8 form two four-digit numbers so that all 4 digits are used in the notation of each number. Calculate the difference between such largest even number and smallest odd number (in that order). - Natural numbers
 Find the number of all natural numbers greater than 200 in which the digits 1, 2, 4, 6, 8 occur at most once and not contains any other digits.
Find the number of all natural numbers greater than 200 in which the digits 1, 2, 4, 6, 8 occur at most once and not contains any other digits. - Half-planes 36831
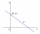 The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest.
The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest. - Restriction 7442
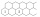 The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top
The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Smallest 4692
 A. Find the largest natural number by which the numbers 54 and 72 can be divided (120, 60, and 42) B. Find the smallest natural number that can be divided by each of the numbers 36 and 48 (24,18 and 16)
A. Find the largest natural number by which the numbers 54 and 72 can be divided (120, 60, and 42) B. Find the smallest natural number that can be divided by each of the numbers 36 and 48 (24,18 and 16)
