Z9–I–1
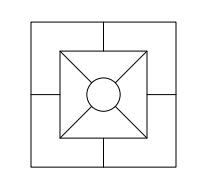
Ve všech devíti polích obrazce mají být vyplněna přirozená čísla tak, aby platilo:
• každé z čísel 2, 4, 6 a 8 je použito alespoň jednou,
• čtyři z polí vnitřního čtverce obsahují součiny čísel ze sousedících polí vnějšího čtverce,
• v kruhu je součet čísel ze sousedících polí vnitřního čtverce.
Zjistěte, které nejmenší a které největší číslo může být napsáno v kruhu.
• každé z čísel 2, 4, 6 a 8 je použito alespoň jednou,
• čtyři z polí vnitřního čtverce obsahují součiny čísel ze sousedících polí vnějšího čtverce,
• v kruhu je součet čísel ze sousedících polí vnitřního čtverce.
Zjistěte, které nejmenší a které největší číslo může být napsáno v kruhu.
Správná odpověď:
Zobrazuji 21 komentářů:
Žák
Prosím Vás nevím jak do vnějších čtverců, pokud čísla nebudou 2 -ciferná, dostat všechna, aby u vnitřních čtverců vznikly nuly a tím pádem i uprostřed?
Žák
Prosím Vás nevím jak do vnějších čtverců, pokud čísla nebudou 2 -ciferná, dostat všechna, aby u vnitřních čtverců vznikly nuly a tím pádem i uprostřed?
Stabil
min = 14 pro vnejsi ctverec s kombinaci cisel 3,2,4,0
max = nekonecno pro vnejsi ctverec s kombinaci cisel 3,2,4,nekonecno
max = nekonecno pro vnejsi ctverec s kombinaci cisel 3,2,4,nekonecno
8 let 1 Like
Žák
min - byl bych spíše pro 3,2,4,1, protože v MO nulu nepočítají jako přirozené číslo
max - nevím jestli lze počítat nekonečno mezi přirozené čísla
max - nevím jestli lze počítat nekonečno mezi přirozené čísla
Jakmel-42
@Zuzii: Vyšlo mi to stejně. Ovšem nemohu to nijak ověřit, názory kolem nás se dost různí.
Žák
Min je 21.
Max nekonečno jak píše Stabil, jelikož jedno číslo můžete ve vnějším čtverci nahradit ,kterým koliv číslem a přitom splníte podmínky za pomoci 3 čísel.
Max nekonečno jak píše Stabil, jelikož jedno číslo můžete ve vnějším čtverci nahradit ,kterým koliv číslem a přitom splníte podmínky za pomoci 3 čísel.
Šíny
Jako min. číslo bych dala 9 ---> 2,4,0,3
ale jestliže MO nebere nulu jako přirozené číslo, tak by mi vyšlo 12 ---> 2,4,3,3
U max. mám nekonečno
ale jestliže MO nebere nulu jako přirozené číslo, tak by mi vyšlo 12 ---> 2,4,3,3
U max. mám nekonečno
8 let 2 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Na papíře
Na papíře bylo napsáno několik kladných celých čísel. Miška si pamatovala pouze to, že každé číslo bylo polovinou součtu všech ostatních čísel. Kolik čísel mohlo být napsaných na papíře? - Představují 82998
Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být - C–I–4 MO 2017
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Prvočísla - 6c
Najít všechna šesticiferná prvočísla, která obsahují každou z číslic 1,2,4,5,7 a 8 právě jednou. Kolik jich je?
- Z8 MO 2021
V dané skupině čísel je jedno číslo rovno průměru všech, největší číslo je o 7 větší než průměr, nejmenší je o 7 menší než průměr a většina čísel ze skupiny má podprůměrnou hodnotu. Jaký nejmenší počet čísel může být ve skupině? - Čtyřciferných 79614
Určete počet všech čtyřciferných přirozených čísel, v dekadickém zápisu, ve kterých není číslice 0 a ze zbývajících devíti čísel se v něm každá nachází nejvýše jednou. - Mirek a Zuzka
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m
