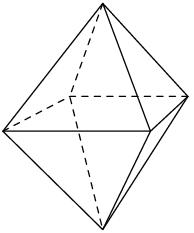
Octahedron - sum
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which also added up.
What values may the resulting sum have?
What values may the resulting sum have?
Final Answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetricsbasic operations and conceptsnumbersUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- SKMO
Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product. - Rhombus angles
If one angle in the rhombus is 137.6°, what is its neighboring angle in the rhombus? - Semicircles
In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o - Octahedron
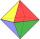All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron. - Remaining 5534
On the table lay eight cards with the numbers 2,3,5,7,11,13,17,19. Fero chose three cards. He added the numbers written on them and found that their sum was 1 more than the sum of the numbers on the remaining cards. Which cards could have been left on the - Built-up area
John build-up area 4.3 x 6.3 = 27.09 m² with building with a wall thickness 25 cm. How many centimeters would he have to subtract from the thickness of the walls that the built-up area fell by 5%? - David number
Jane and David train in the addition of decimal numbers so that each of them will write a single number, and these two numbers will then be added up. The last example was 11.11. David's number also had the same number of digits before and after a point. J
