Osmistěn
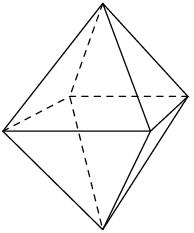
Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také sečetl.
Jakých hodnot může tento výsledný součet nabývat?
Jakých hodnot může tento výsledný součet nabývat?
Správná odpověď:
Zobrazuji 7 komentářů:
Žák
Stále mi to není jasné. Osmistěn, tedy 8 stěn - sčítáme stěnu + 3 sousední - tedy 4 čísla dají jeden součet a součtů je osm - tedy každé číslo je tam 4x, musíme 36 násobit 4. Kde dělám chybu?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriezákladní operace a pojmyčíslaJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Spotřeboval 48761
Matouš maluje svůj pokoj. Maluje stěny tvaru čtverce. Když vymaloval stěnu se stranou 3 m, spotřeboval 5kg barvy. Kolik kg barvy bude potřebovat na zeď o straně délky 6 m? - Tapety
Stěny pokoje mají být polepeny tapetami od podlahy až ke stropu. Pokoj má obdélníkový tvar. Je široký 3m, dlouhý 5m a 2,5m vysoký. V jedné stěně jsou dveře, které i se zárubněmi zaujímají obdélník o rozměrech 80cm a 2m. V místnosti je také jedno okno. I s - MO Z7–I–3 2019
Roman má rád kouzla a matematiku. Naposled kouzlil s trojmístnými nebo čtyřmístnými čísly takto: • z daného čísla vytvořil dvě nová čísla tak, že ho rozdělil mezi číslicemi na místě stovek a desítek (např. Z čísla 581 by dostal 5 a 81), • nová čísla sečet - Představují 82998
Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být - Petra 3 MO 2022 Petra měla napsaná přirozená čísla od 1 do 9. Dvě z těchto čísel sečetla, smazala a výsledný součet napsala místo sčítanců. Měla tak napsáno osm čísel, která se jí podařilo rozdělit do dvou skupin se stejným součinem. Určete jaký největší mohl být tento s
- Z5–I–6 MO 2017
Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech - Pravděpodobnost 83596 V loterii si člověk náhodně vybere čtyři různá přirozená čísla od 1 do 10 a pokud se tato čtyři čísla shodují se čtyřmi čísly, která již určila loterijní komise, vyhrává cenu. Jaká je pravděpodobnost výhry ve hře? (Pořadí čísel není důležité).
