Osemsten súčet
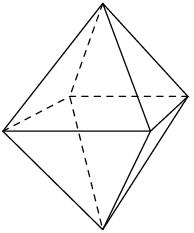
Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré tiež spočítal.
Akých hodnôt môže tento výsledný súčet nadobúdať?
Akých hodnôt môže tento výsledný súčet nadobúdať?
Správna odpoveď:
Zobrazujem 2 komentáre:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaplanimetriazákladné operácie a pojmyčíslaJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Na stene
Na stene bolo napísané dvakrát to isté päťciferné číslo. Jožo pred jeden zápis čísla pripísal jednotku. Fero pripísal jednotku za ten druhý zápis čísla. Tým dostali dve šesťciferné čísla, z ktorých bolo jedno trikrát väčšie ako druhé. Ktoré päťciferné čís - Obdĺžnik - kto má pravdu
Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3. Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto - Z7–I–1 MO 2018
Na každej z troch kartičiek je napísaná jedna cifra rôzna od nuly (na rôznych kartičkách nie sú nutne rôzne cifry). Vieme, že akékoľvek trojciferné číslo zložené z týchto kartičiek je deliteľné šiestimi. Navyše možno z týchto kartičiek zložiť trojciferné - MO 2022
Petra mala napísané prirodzené čísla od 1 do 9. Dve z týchto čísel sčítala, zmazala a výsledný súčet napísala miesto sčítancov. Mala tak napísané osem čísel, ktoré sa jej podarilo rozdeliť do dvoch skupín s rovnakým súčinom. Určite aký najväčší mohol byť - Z5–I–6 MO 2017
Na stole ležalo osem kartičiek s číslami 2,3,5,7,11,13,17,19. Fero si vybral tri kartičky. Sčítal na nich napísané čísla a zistil, že ich súčet je o 1 väčší ako súčet čísel na zvyšných kartičkách. Ktoré kartičky mohli zostať na stole? Určte všetky možnost - Lotéria V lotérii si človek náhodne vyberie štyri rôzne prirodzené čísla od 1 do 10 a ak sa tieto štyri čísla zhodujú so štyrmi číslami, ktoré už určila lotériová komisia, vyhráva cenu. Aká je pravdepodobnosť výhry v hre? (Poradie čísel nie je dôležité).
- Adam MO (asi MO Z8) Adam napísal nasledujúci súčet s piatimi tajnými sčítancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré najväčšie číslo môž
