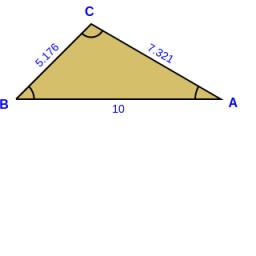
Angles
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β?
Final Answer:
Showing 1 comment:
Math Lover
Can you help me with this (The drawing will be provided. HINT. Use the difference of squares formula a- = (a - b)(a + b). Let AABC be a right-angled triangle with the right angle in A and base BC 50 •6 meters. Let AD be the beight correspond- ing to BC. II AB 30 •6 meters and BD= 18•6 meters, find: AC , DC, AD)
Tips for related online calculators
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Similarity coefficient
 The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'.
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'. - The triangles
 The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '.
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Inner angles
 The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi
The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi - Exterior angles
 In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC.
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - Angle at the apex
 In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles?
In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles? - Triangle from median
 Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5. - Triangle - angles
 ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles?
ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles?
