Sequence
In the arithmetic sequence, is a1=-1, d=4. Which member is equal to the number 203?
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Geometric sequence
 In the geometric sequence is a4 = 20 a9 = -160. Calculate the first member a1 and quotient q.
In the geometric sequence is a4 = 20 a9 = -160. Calculate the first member a1 and quotient q. - AP - basics
 Determine the first member and differentiate the following sequence: a3-a5=24 a4-2a5=61
Determine the first member and differentiate the following sequence: a3-a5=24 a4-2a5=61 - Tenth member
 Calculate the tenth member of the geometric sequence when given: a1=1/2 and q=2
Calculate the tenth member of the geometric sequence when given: a1=1/2 and q=2 - GP members
 The geometric sequence has ten members. The last two members are 2 and -1. Which member is -1/16?
The geometric sequence has ten members. The last two members are 2 and -1. Which member is -1/16?
- Determine 2388
 Determine the fifth member of the sequence if a1 = -32, q = 21
Determine the fifth member of the sequence if a1 = -32, q = 21 - Geometric sequence 5
 About members of the geometric sequence, we know: 3 a5:a3 = 27:25 7 a3 +5 a7 = 1 : 564 Calculate a1 (first member) and q (common ratio or q-coefficient)
About members of the geometric sequence, we know: 3 a5:a3 = 27:25 7 a3 +5 a7 = 1 : 564 Calculate a1 (first member) and q (common ratio or q-coefficient) - Nineteenth member
 Find the nineteenth member of the arithmetic sequence: a1=33 d=5 find a19
Find the nineteenth member of the arithmetic sequence: a1=33 d=5 find a19 - Three-member 69274
 The teacher wants to create one three-member team of four girls and four boys, in which there will be one girl and two boys. How many different options does it have to create a team?
The teacher wants to create one three-member team of four girls and four boys, in which there will be one girl and two boys. How many different options does it have to create a team? - Arithmetic 81811
 In which arithmetic sequence is the sum of the first five terms with odd indices equal to 85 and the sum of the first five terms with even indices equal to 100?
In which arithmetic sequence is the sum of the first five terms with odd indices equal to 85 and the sum of the first five terms with even indices equal to 100?
- AP with variables
 What is the second member in the arithmetic sequence with 7 terms, whose first and last terms are x+2y and 7x-4y
What is the second member in the arithmetic sequence with 7 terms, whose first and last terms are x+2y and 7x-4y - Sequence 3
 Write the first 5 members of an arithmetic sequence: a4=-35, a11=-105.
Write the first 5 members of an arithmetic sequence: a4=-35, a11=-105. - AS sequence
 In an arithmetic sequence is given the difference d = -3 and a71 = 455. a) Determine the value of a62 b) Determine the sum of 71 members.
In an arithmetic sequence is given the difference d = -3 and a71 = 455. a) Determine the value of a62 b) Determine the sum of 71 members. - Sequence 13
 2, 2, 3, 5, 9, 11, 17, 21 If the number 23 is added to the list, which measurement will NOT change?
2, 2, 3, 5, 9, 11, 17, 21 If the number 23 is added to the list, which measurement will NOT change? - Arithmetic 81795
 In which arithmetic sequence is S5=S6=60?
In which arithmetic sequence is S5=S6=60?
- Sequence 5535
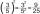 Find the value of the third member of the sequence if the sequence is given by: 3^n + 93.
Find the value of the third member of the sequence if the sequence is given by: 3^n + 93. - Geometric sequence 3
 In geometric sequence is a8 = 312500; a11= 39062500; sn=1953124. Calculate the first item a1, quotient q, and n - number of members by their sum s_n.
In geometric sequence is a8 = 312500; a11= 39062500; sn=1953124. Calculate the first item a1, quotient q, and n - number of members by their sum s_n. - Arithmetic 81808
 An increasing arithmetic sequence has an odd number of terms. The middle term is 302. If we remove the 4 largest terms from the sequence, the middle term will be 296. Determine the difference in the sequence.
An increasing arithmetic sequence has an odd number of terms. The middle term is 302. If we remove the 4 largest terms from the sequence, the middle term will be 296. Determine the difference in the sequence.
