Two trains
Through the bridge, long l = 240m, the train passes through the constant speed at time t1 = 21s. A train running along the traffic lights at the edge of the bridge passes the same speed at t2 = 9s.
a) What speed v did the train go?
b) How long did a train driver cross the bridge take?
c) What is the L train length?
d) How long will it take for a train to overtake in the same direction with the same length but half the speed?
e) How long will it take for a train to overtake in the opposite direction with the same length but half the speed?
a) What speed v did the train go?
b) How long did a train driver cross the bridge take?
c) What is the L train length?
d) How long will it take for a train to overtake in the same direction with the same length but half the speed?
e) How long will it take for a train to overtake in the opposite direction with the same length but half the speed?
Correct answer:

Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Do you want to convert length units?
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The enrolment 2
 The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment? - Violin and dance lesson
 Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of
Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of - EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Vertex of the rectangle
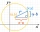 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
- Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - The tangent of the hyperbola
 Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Quadratic equation - Viets
 In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas.
In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas. - Two containers 2
 Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on
Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on - The sum 41
 The sum of 640.00 was deposited in the first bank for five years, and the interest given was 160.00. Find the rate.
The sum of 640.00 was deposited in the first bank for five years, and the interest given was 160.00. Find the rate.
- Properties of eq2 roots
 If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq. - Fredrik
 Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b.
Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b. - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - Flower shop
 In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost
In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost - Evaluate complex eq
 If z=x+yi and 3x+(3x-y)i=4-6i then z=
If z=x+yi and 3x+(3x-y)i=4-6i then z=
- Domino
 Domino and Winnie share some biscuits. The ratio of biscuits between them was 4:3. Domino gave Winnie 5 biscuits, and the ratio changed to 1:2. How many biscuits are in total?
Domino and Winnie share some biscuits. The ratio of biscuits between them was 4:3. Domino gave Winnie 5 biscuits, and the ratio changed to 1:2. How many biscuits are in total? - A barrel
 A barrel of sorghum weighs 56kg. The same barrel filled with kerosene weighs 35kg. If sorghum is twice as heavy as kerosene, how much does the empty barrel weigh?
A barrel of sorghum weighs 56kg. The same barrel filled with kerosene weighs 35kg. If sorghum is twice as heavy as kerosene, how much does the empty barrel weigh? - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
