Area + volume - practice problems
Number of problems found: 793
- Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be? - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A frustum
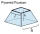 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
- The volume 9
 The volume of a large tank is 210 yd³. its 2 2/5 yd wide and 2 4/5 yd high. What is the length of the tank?
The volume of a large tank is 210 yd³. its 2 2/5 yd wide and 2 4/5 yd high. What is the length of the tank? - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Anneta
 Anneta wants to buy a piece of land for farming; she wants to use 1/3 of the land to plant cocoa, 2/7 for a Palm plantation, and the rest for a vegetable plantation. 1). Find the fractions of the land used for vegetable plantation 2). If one wants to use
Anneta wants to buy a piece of land for farming; she wants to use 1/3 of the land to plant cocoa, 2/7 for a Palm plantation, and the rest for a vegetable plantation. 1). Find the fractions of the land used for vegetable plantation 2). If one wants to use - Create 6
 Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
- The cup
 In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure.
In a measuring cup set, the cup measure is 6 cm wide. The set also contains a 1-cup measure and a cup measure, both of which are similar in shape to the cup measure. Find the width of: a) 1/2 cup b) the 1 cup measure c) the 1/3 cup measure. - Poured liquid
 If I pour 59ml of liquid into an area of 594 sq mm, how thick would the liquid be?
If I pour 59ml of liquid into an area of 594 sq mm, how thick would the liquid be? - Length 83358
 A block-shaped pool has a length of 50m, width of 25m, and depth of 3.5 m. When the pool is filled 50 cm below the edge, how many hectoliters of water is in it? If we paint the inside of the pool two coats and you pay 50 cents per 1m2, how much
A block-shaped pool has a length of 50m, width of 25m, and depth of 3.5 m. When the pool is filled 50 cm below the edge, how many hectoliters of water is in it? If we paint the inside of the pool two coats and you pay 50 cents per 1m2, how much - Abundantly 83354
 If 10 mm of water fell on a trapezoid-shaped garden with bases of 30 m and 20 m and a height of 20 m, how many buckets of water would we need to water the garden equally abundantly if the bucket had a volume of 15 l?
If 10 mm of water fell on a trapezoid-shaped garden with bases of 30 m and 20 m and a height of 20 m, how many buckets of water would we need to water the garden equally abundantly if the bucket had a volume of 15 l? - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
- Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Calculate 83311
 The surface of the cuboid is S = 1714 cm². The edges are 25 and 14 cm long. Calculate its volume.
The surface of the cuboid is S = 1714 cm². The edges are 25 and 14 cm long. Calculate its volume. - Cylinder's 83288
 Calculate the radius of the cylinder's base if its volume is equal to 12.56 cm².
Calculate the radius of the cylinder's base if its volume is equal to 12.56 cm². - Quadrilateral 83272
 Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm.
Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm. - Quadrilateral 83254
 What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm?
What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Tip: Our volume units converter will help you convert volume units. Area - practice problems. Volume - practice problems.
