Practice problems of the volume of a cone
Number of problems found: 156
- A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Rotating cone
 The rotating cone has a base diameter of 18 dm and a height of 12 dm. Calculate the volume V.
The rotating cone has a base diameter of 18 dm and a height of 12 dm. Calculate the volume V. - Rotating cone
 Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm.
Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm. - Ice cream in cone
 The ice cream cone with a diameter of 5.6 cm is 0.5 dl of ice cream. Calculate the depth of the cone.
The ice cream cone with a diameter of 5.6 cm is 0.5 dl of ice cream. Calculate the depth of the cone.
- Hard cone problem
 The cone's surface is 200 cm², and its height is 7 centimeters. Calculate the volume of this cone.
The cone's surface is 200 cm², and its height is 7 centimeters. Calculate the volume of this cone. - Volume of the cone
 Find the volume of the cone with the base radius r and the height v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm
Find the volume of the cone with the base radius r and the height v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Calculate 30991
 The volume of the cone is 461.58 cm³. Its diameter is 14 cm. Calculate the surface area of this cone.
The volume of the cone is 461.58 cm³. Its diameter is 14 cm. Calculate the surface area of this cone. - Children's 8246
 We prepare a pile of sand in the shape of a cone with a height of 1 m and a diameter of 1.6 m. We prepare it for the children's sandpit. What volume of sand does this pile occupy?
We prepare a pile of sand in the shape of a cone with a height of 1 m and a diameter of 1.6 m. We prepare it for the children's sandpit. What volume of sand does this pile occupy? - The volume
 The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
- Surface area
 The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone.
The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone. - Cross-sections of a cone
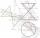 Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body.
Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Cone-shaped 43291
 Calculate the volume and weight of a pile of cone-shaped sand with a diameter of 8m and a height of v = 4.5m, the density of sand is 1500kg / M cubic
Calculate the volume and weight of a pile of cone-shaped sand with a diameter of 8m and a height of v = 4.5m, the density of sand is 1500kg / M cubic - Circumference 27581
 The rotating cone has a base circumference of 62.8 cm. And a height of 0.7 dm. Calculate its surface area and volume.
The rotating cone has a base circumference of 62.8 cm. And a height of 0.7 dm. Calculate its surface area and volume. - Calculate 16513
 The conical funnel has a volume of 0.5 liters and a height of 7 cm. Calculate the radius of its upper edge.
The conical funnel has a volume of 0.5 liters and a height of 7 cm. Calculate the radius of its upper edge.
- Bottles of juice
 How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm?
How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm? - Cone-shaped 8170
 How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer.
How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer. - Without 8260
 The ice cream sundae glass has a cone shape. Its height without legs is 9 cm, and its radius is 5 cm. Šimon bought eight scoops of ice cream, which all melted in the sun. One scoop of ice cream has a volume of 32 cm³. How many cm³ of melted ice cream will
The ice cream sundae glass has a cone shape. Its height without legs is 9 cm, and its radius is 5 cm. Šimon bought eight scoops of ice cream, which all melted in the sun. One scoop of ice cream has a volume of 32 cm³. How many cm³ of melted ice cream will - Determine 3784
 The teacher brought to class two wooden models of cones, which were made of the same type of wood. The first model weighed 800g. The other had twice the base radius but half the height. Determine the mass of the second cone in grams.
The teacher brought to class two wooden models of cones, which were made of the same type of wood. The first model weighed 800g. The other had twice the base radius but half the height. Determine the mass of the second cone in grams. - Castle model
 The castle model has a cone-shaped roof. The cone side is 45 cm long, and the base radius is 27 cm. a) What is the roof volume? b) How many dm² of wallpaper is used to glue the roof, i.e., the cone shell? c) What is the weight of the roof if it is made of
The castle model has a cone-shaped roof. The cone side is 45 cm long, and the base radius is 27 cm. a) What is the roof volume? b) How many dm² of wallpaper is used to glue the roof, i.e., the cone shell? c) What is the weight of the roof if it is made of
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
