Reason - math word problems - page 30 of 108
Number of problems found: 2157
- Pagans
 Jano and Michael ate pagans. Jano ate three more than Michael. The product of their counts (numbers) is 180. How many pagans did each of them eat?
Jano and Michael ate pagans. Jano ate three more than Michael. The product of their counts (numbers) is 180. How many pagans did each of them eat? - One dice
 Calculate the probability of one dice roll with the numbers 1, 2, 3, 4, 5, and 6 on the walls. Write the results in a notebook in the shape of a fraction in the basic form: 2/3. a, The number 1 falls on the cube. b, The number 5 falls on the cube. c, An e
Calculate the probability of one dice roll with the numbers 1, 2, 3, 4, 5, and 6 on the walls. Write the results in a notebook in the shape of a fraction in the basic form: 2/3. a, The number 1 falls on the cube. b, The number 5 falls on the cube. c, An e - Three dice
 The player throwing the three dice asked G. Galilei: "Should I bet on the sum of 11 or the sum of 12?" What did Galilei answer him? Hint: write down all three triples of numbers that can be thrown, have a total of 11, have a total of 12, and compare proba
The player throwing the three dice asked G. Galilei: "Should I bet on the sum of 11 or the sum of 12?" What did Galilei answer him? Hint: write down all three triples of numbers that can be thrown, have a total of 11, have a total of 12, and compare proba - Telco company
 The upstairs communications company offers customers a special long-distance calling rate that includes a $0.10 per minute charge. Which of the following represents this fee schedule, where m represents the number of minutes and c is the call's overall co
The upstairs communications company offers customers a special long-distance calling rate that includes a $0.10 per minute charge. Which of the following represents this fee schedule, where m represents the number of minutes and c is the call's overall co - Into box
 How many cubes with an edge of 2.5 cm fit into a box measuring 11.6 cm, 8.9 cm, and 13.75 cm?
How many cubes with an edge of 2.5 cm fit into a box measuring 11.6 cm, 8.9 cm, and 13.75 cm? - Light bulbs
 You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb
You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb - Repeated 33571
 Use the digits 3, 4, 5, and 6 to write all even numbers. How many such numbers can you write when you can repeat the numbers?
Use the digits 3, 4, 5, and 6 to write all even numbers. How many such numbers can you write when you can repeat the numbers? - Themselves 33561
 How many ways can a 6-member football club member choose a leader and captain from among themselves?
How many ways can a 6-member football club member choose a leader and captain from among themselves? - Number 4
 Kamila wrote all-natural numbers from 1 to 400 inclusive. How many times did she write the number 4?
Kamila wrote all-natural numbers from 1 to 400 inclusive. How many times did she write the number 4? - Sphere cut
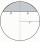 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Deceleration of car
 The car has a speed of 60 km/h and, after a 100 m journey speed of 40 km/h. What is the deceleration of a car if we assume that its movement is constantly slowed down?
The car has a speed of 60 km/h and, after a 100 m journey speed of 40 km/h. What is the deceleration of a car if we assume that its movement is constantly slowed down? - Two-element combinations
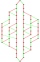 Write all two-element combinations from elements a, b, c, and d.
Write all two-element combinations from elements a, b, c, and d. - Fresh juice
 The seller offers fresh-squeezed juice, which the customer either pours into his own containers or sells in liter plastic bottles, which the customer buys from him. A liter of juice costs 40 CZK more than a bottle. There is no charge for turning the juice
The seller offers fresh-squeezed juice, which the customer either pours into his own containers or sells in liter plastic bottles, which the customer buys from him. A liter of juice costs 40 CZK more than a bottle. There is no charge for turning the juice - Borrowing bicycle
 Jakub lent a bicycle to friends who wanted to ride it. For a three-hour bike ride, Jakub received two chocolates. Yup. If you wanted a bike for 2 hours, you had to give Jakub 12 candies. Peter gave Jakub 1 chocolate and three candies. How long can Peter r
Jakub lent a bicycle to friends who wanted to ride it. For a three-hour bike ride, Jakub received two chocolates. Yup. If you wanted a bike for 2 hours, you had to give Jakub 12 candies. Peter gave Jakub 1 chocolate and three candies. How long can Peter r - Three-digit 33263
 Calculate the difference between the smallest odd four-digit number and the largest even three-digit number, where we can form each number from only these digits: 0, 1, 3, 5, 7, 8, 9 without repeating digits.
Calculate the difference between the smallest odd four-digit number and the largest even three-digit number, where we can form each number from only these digits: 0, 1, 3, 5, 7, 8, 9 without repeating digits. - Competition 33041
 The long-term volleyball tournament is played one-on-one. So far, 11 teams have entered the competition. How many matches will be lost when two teams unsubscribe?
The long-term volleyball tournament is played one-on-one. So far, 11 teams have entered the competition. How many matches will be lost when two teams unsubscribe? - Aleš coins
 Aleš has one coin, Boris and Cyril each have two coins. Aleš has 5 Sk more than Boris and 5 Sk less than Cyril. Note Czech coins are 1, 2, 5, 10, 20, 50 Sk. Aleš has ___ Sk. Boris has ___ Sk and ___ Sk. Cyril has ___ Sk and ___ Sk. Together, they have ___
Aleš has one coin, Boris and Cyril each have two coins. Aleš has 5 Sk more than Boris and 5 Sk less than Cyril. Note Czech coins are 1, 2, 5, 10, 20, 50 Sk. Aleš has ___ Sk. Boris has ___ Sk and ___ Sk. Cyril has ___ Sk and ___ Sk. Together, they have ___ - Ascending 32663
 How many natural numbers can you make from the digits in 4052? No digit may be repeated in the number entry. Sort the numbers in ascending order of size.
How many natural numbers can you make from the digits in 4052? No digit may be repeated in the number entry. Sort the numbers in ascending order of size. - Divisible by nine
 How many three-digit natural numbers in total are divisible without a remainder by the number 9?
How many three-digit natural numbers in total are divisible without a remainder by the number 9? - Distribute 32451
 The king cannot decide how to distribute 4 cubes of pure gold, which have edges of length 3cm, 4cm, 5cm, and 6cm, to two sons as fairly as possible. Design a solution so that the cubes do not have to be cut.
The king cannot decide how to distribute 4 cubes of pure gold, which have edges of length 3cm, 4cm, 5cm, and 6cm, to two sons as fairly as possible. Design a solution so that the cubes do not have to be cut.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
