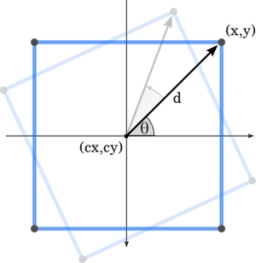
Coordinates of square vertices

I have coordinates of square vertices A / -3; 1/and B/1; 4 /. Find coordinates of vertices C and D, C 'and D'. Thanks Peter.

Correct answer:

x₂ =  2.9696
y₂ =  -0.5957
x₃ =  -1.0304
y₃ =  -3.5957
x₄ =  -0.9696
y₄ =  8.5957
x₅ =  -4.9696
y₅ =  5.5957

Step-by-step explanation:

$$\begin{gathered} x_0=-3 \\ {y}_0=1 \\ {x}_1=1 \\ {y}_1=4 \\ a=\sqrt{(x_0-x_1{)}^2+(y_0-y_1{)}^2}=\sqrt{((-3)-1{)}^2+(1-4{)}^2}=5 \\ \tan \alpha ={\displaystyle \frac{y_0-y_1}{x_0-y_1}}={\displaystyle \frac{1-4}{(-3)-4}}={\displaystyle \frac{3}{7}}\doteq 0.4286 \\ \alpha =\arctan ({\displaystyle \frac{y_0-y_1}{x_0-y_1}})=\arctan ({\displaystyle \frac{1-4}{(-3)-4}})\doteq 0.4049\text{ rad } \\ {d}_x=a\cdot \cos (\alpha )=5\cdot \cos (0.4049)\doteq 4.5957 \\ {d}_y=a\cdot \sin (\alpha )=5\cdot \sin (0.4049)\doteq 1.9696 \\ {x}_2=x_1+d_y=1+1.9696=2.9696 \end{gathered}$$

$y_2=y_1-d_x=4-4.5957=-0.5957$

$x_3=x_0+d_y=(-3)+1.9696=-1.0304$

$y_3=y_0-d_x=1-4.5957=-3.5957$

$x_4=x_1-d_y=1-1.9696=-0.9696$

$y_4=y_1+d_x=4+4.5957=8.5957$

$x_5=x_0-d_y=(-3)-1.9696=-4.9696$

$$\begin{gathered} y_5=y_0+d_x=1+4.5957\doteq 5.5957=5.5957 \\ {a}_2=\sqrt{(x_0-x_3{)}^2+(y_0-y_3{)}^2}=\sqrt{((-3)-(-1.0304){)}^2+(1-(-3.5957){)}^2}=5 \\ {a}_3=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}=\sqrt{(1-2.9696{)}^2+(4-(-0.5957){)}^2}=5 \\ {a}_4=\sqrt{(x_2-x_3{)}^2+(y_3-y_2{)}^2}=\sqrt{(2.9696-(-1.0304){)}^2+((-3.5957)-(-0.5957){)}^2}=5 \\ {b}_2=\sqrt{(x_0-x_5{)}^2+(y_0-y_5{)}^2}=\sqrt{((-3)-(-4.9696){)}^2+(1-5.5957{)}^2}=5 \\ {b}_3=\sqrt{(x_1-x_4{)}^2+(y_1-y_4{)}^2}=\sqrt{(1-(-0.9696){)}^2+(4-8.5957{)}^2}=5 \\ {b}_4=\sqrt{(x_4-x_5{)}^2+(y_4-y_5{)}^2}=\sqrt{((-0.9696)-(-4.9696){)}^2+(8.5957-5.5957{)}^2}=5 \end{gathered}$$

Try another example

Related math problems and questions:

• Coordinates of square vertices
  The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
• Space vectors 3D
  The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, the distance between the vectors.
• Right angled triangle 3
  Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find its unknown sides length.
• Three points
  Three points K (-3; 2), L (-1; 4), M (3, -4) are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write the d
• Right
  Determine angles of the right triangle with the hypotenuse c and legs a, b, if: ?
• Diagonals of a prism
  The base of the square prism is a rectangle with dimensions of 3 dm and 4 dm. The height of the prism is 1 m. Find out the angle between the body diagonal with the diagonal of the base.
• Medians and sides
  Triangle ABC in the plane Oxy; are the coordinates of the points: A = 2.7 B = -4.3 C-6-1 Try calculate lengths of all medians and all sides.
• Resultant force
  Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25°
• Trigonometric functions
  In the right triangle is: ? Find the value of s and c: ? ?
• Vertices of a right triangle
  Show that the points D(2,1), E(4,0), F(5,7) are vertices of a right triangle.
• Triangle
  Plane coordinates of vertices: K[11, -10] L[10, 12] M[1, 3] give Triangle KLM. Calculate its area and its interior angles.
• Ratio iso triangle
  The ratio of the sides of an isosceles triangle is 7:6:7 Find the base angle to the nearest answer correct to 3 significant figure.
• Distance of points
  A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
• Right angled triangle 2
  LMN is a right-angled triangle with vertices at L(1,3), M(3,5), and N(6,n). Given angle LMN is 90° find n
• Trapezoid MO
  The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of ​​the trapezoid.
• Vertices of RT
  Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle.
• CoG center
  Find the position of the center of gravity of a system of four mass points having masses, m₁, m₂ = 2 m1, m₃ = 3 m1, and m₄ = 4 m₁, if they lie at the vertices of an isosceles tetrahedron. (in all cases, between adjacent material points, the distance