Mám vrcholy
Mám vrcholy čtverce A/-3;1/a B/1;4/. Urči souřadnice vrcholů C a D, C' a D'. Díky Petr.
Vaše odpověď:
Vaše odpověď:
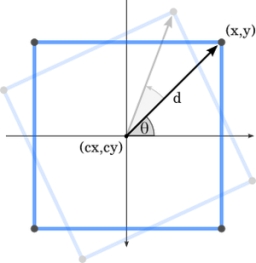
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetriezákladní operace a pojmygoniometrie a trigonometrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Tři 237
Tři vrcholy obdélníku mají souřadnice (5, 3), (5, -1), (-1, -1). Jaké jsou souřadnice čtvrtého vrcholu obdélníku? - Šipky - souřadnice Trojúhelník má vrcholy na (4, 5), (-3, 2) a (-2, 5). Jaké jsou souřadnice vrcholů obrazu po přeložení (x, y) šipka-vpravo (x + 3, y - 5)?
- Těžiště
Vrcholy trojúhelníku ABC mají od přímky p po řadě vzdálenost 3 cm, 4 cm a 8 cm. Urči vzdálenost těžiště trojúhelníku od přímky p. - Souřadnice vrcholů
Trojúhelník PQR má vrcholy umístěné na souřadnicích (2, 2), (5, -4) a (-4, -1). Jaký typ trojúhelníku je trojúhelník PQR? - Vrcholy trojúhelníku
Určete souřadnice vrcholu trojúhelníku ABC, známe-li středy SAB [0;3] SBC [1;6] SAC [4;5], jeho stran AB, BC, AC. - Čtverec 28
Čtverec ABCD má střed S[−3, −2] a vrchol A[1, −3]. Určete souřadnice ostatních vrcholů čtverce. - Souřadnice - vrcholy
Souřadnice dvou vrcholů rovnostranného trojúhelníku jsou (1,1) a (5,1). Jaké jsou souřadnice třetího vrcholu?
