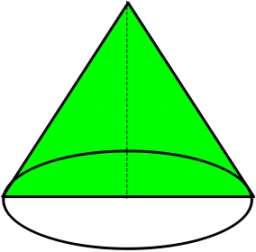
Axial section of the cone
The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cone
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- basic functions
- ratio
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Axial section
Calculate the volume and surface of a cone whose axial section is an equilateral triangle with side length a = 18cm. - Cone side
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Equilateral 73374
The axial section of the cone is an equilateral triangle with a side of 12 cm. Surface and volume calculation. - Calculate 4842
The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm.
- Axial section
The axial section of the cone is an equilateral triangle with an area 208 m². Calculate the volume of the cone. - Axial section
The axial section of the cylinder is diagonal 45 cm long, and we know that the area of the side and the base area are in ratio 6:5. Calculate the height and radius of the cylinder base. - Angle of cone
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
