Hollow sphere
The steel hollow sphere floats on the water plunged into half its volume. Determine the outer radius of the sphere and wall thickness, if you know that the weight of the sphere is 0.5 kg and the density of steel is 7850 kg/m3
Correct answer:

Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Grain storage
 On their farm, Adam's family maintains a storage facility that can hold 19.2 cubic yards (yd3) of grain. Since 1 yard is approximately equal to 0.9144 m, this volume can be converted to m³.
On their farm, Adam's family maintains a storage facility that can hold 19.2 cubic yards (yd3) of grain. Since 1 yard is approximately equal to 0.9144 m, this volume can be converted to m³. - Two numbers 17
 The sum of two numbers is 9, and the sum of their cubes is 189; find the sum of their squares.
The sum of two numbers is 9, and the sum of their cubes is 189; find the sum of their squares. - Vegetable storage
 To help vegetables stay fresh longer, Liam's family maintains storage near their home. The total volume of the root cellar is 737 cubic feet (ft³). Use the fact that 1 foot is approximately equal to 0.3048 m to convert this volume to m³. Round your answer
To help vegetables stay fresh longer, Liam's family maintains storage near their home. The total volume of the root cellar is 737 cubic feet (ft³). Use the fact that 1 foot is approximately equal to 0.3048 m to convert this volume to m³. Round your answer - Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
- A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - A man 12
 A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them
A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them - Smallest z9
 Find the smallest positive numbers a and b for which 7a³ = 11b⁵
Find the smallest positive numbers a and b for which 7a³ = 11b⁵ - FINDING GEOMETRIC MEANS
 Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81]
Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81] - Evaluate 26
 Evaluate square root: √1³+2³+3³+4³=
Evaluate square root: √1³+2³+3³+4³=
- Two pots
 Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot
Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot - Indoor aquarium
 World's biggest indoor aquarium. In its enormous tank with the capacity represented by the following polynomial V=4x³+43x²+63x The aquarium is rectangular prism shape. Find the following: 1. If the aquarium's height is x, then find the area of the base (B
World's biggest indoor aquarium. In its enormous tank with the capacity represented by the following polynomial V=4x³+43x²+63x The aquarium is rectangular prism shape. Find the following: 1. If the aquarium's height is x, then find the area of the base (B - Sphere volume formula
 If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7
If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7 - Jointly and cube power
 If y varies jointly as x and the cube of z and y=16 when x=4 and z=2, find an equation representing this relationship. a. y=xz b. y = 2xz³ c.y = 2kx/z³ d.y = xz³/2
If y varies jointly as x and the cube of z and y=16 when x=4 and z=2, find an equation representing this relationship. a. y=xz b. y = 2xz³ c.y = 2kx/z³ d.y = xz³/2 - Perfect cube
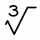 Which of the following number is not a perfect cube? a. 64 b. 729 c. 800 d. 1331
Which of the following number is not a perfect cube? a. 64 b. 729 c. 800 d. 1331
- Height of a cube
 What is the volume of a cube if the height is 5cm?
What is the volume of a cube if the height is 5cm? - An architect 2
 An architect is designing a house. He wants the bedroom to have the dimensions of 8 ft by 4 ft by 7 ft. The architect doubles all three dimensions to create the den. Does that mean the den will have double the volume of the bedroom? First, find the volume
An architect is designing a house. He wants the bedroom to have the dimensions of 8 ft by 4 ft by 7 ft. The architect doubles all three dimensions to create the den. Does that mean the den will have double the volume of the bedroom? First, find the volume - Future value investment
 Poseidon deposited 2,747 golden drachmas in a Mount Olympus college savings account to ensure Percy could attend college. It pays 0.04 (percent in decimal form) annual interest. After 11 years, he withdraws the money. How much more money would he have if
Poseidon deposited 2,747 golden drachmas in a Mount Olympus college savings account to ensure Percy could attend college. It pays 0.04 (percent in decimal form) annual interest. After 11 years, he withdraws the money. How much more money would he have if
