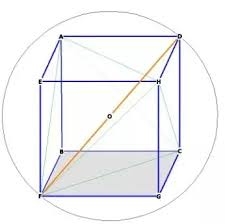
Cube in sphere
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume?
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Clay balls
How many can clay balls with a radius of 1 cm be made from a ball of clay with a radius of 8 cm? - Percentage 3481
We turned a sphere with the largest possible radius from a cube with an edge length of 8 cm. Calculate the volume of the cube, the ball, and the percentage of waste when turning. - Eight
Eight small Christmas balls with a radius of 1 cm have the same volume as one large Christmas ball. What has a bigger surface: eight small balls or one big ball? - Cube in ball
The cube is inscribed into the sphere of radius 181 dm. How many percent is the volume of the cube of the volume of the sphere? - Cube-shaped 81931
A ball with a diameter of 10 cm is in a cube-shaped box with an edge of 10 cm. What percentage of the box does the ball fill? - Percentage + sphere
A sphere G is inscribed in the cube K with the length a. A cube K1 is inscribed in sphere G. What percentage of the volume of cube K is made up of the volume of cube K1? - Plasticine ball
Plasticine balls have a radius r1=85 cm, r2=60 mm, r3=59 cm, r4=86 cm, r5=20 cm, r6=76 mm, r7=81 mm, r8=25 mm, r9=19 mm, r10=14 cm. They are mold
