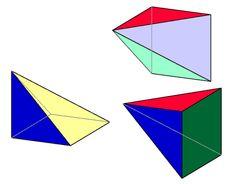
Pyramid
Cuboid ABCDEFGH has dimensions AB 3 cm, BC 4 cm, CG 5 cm. Calculate the volume and surface area of a triangular pyramid ADEC.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- solid geometry
- cuboid
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Circumference 4532
The block ABCDEFGH is given, / AB / = 3.5 cm, / BC / = 4.1 cm, and the circumference of the BCGF wall is 12.4 cm. Calculate the block's area and volume. - Distance of lines
Find the distance of lines AE and CG in cuboid ABCDEFGH if given | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm - Cube 1-2-3
Calculate the volume and surface area of the cube ABCDEFGH if: a) /AB/ = 4 cm b) The perimeter of wall ABCD is 22 cm c) the sum of the lengths of all cube edges is 30 cm. - Calculate 83248
The cube ABCDEFGH has an edge of length 3 cm. Calculate the volume of the pyramid ABCDH.
- ABCDEFGH 82499
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG? - Regular triangular pyramid
Calculate the volume and surface area of the regular triangular pyramid. The height of the pyramid is 12 centimeters. The bottom edge is 4 centimeters, and the height of the sidewall is 12 centimeters. - Triangular 46641
The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
