Two lands
The common area of the two neighboring lands is 964 m2. The second land is smaller by 77 m2, twice the size of the first land. Find the areas of each land.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Land areas
Two land areas are 244 m². The first parcel is 40 m² less than twice the second one. What is the acreage of each parcel? - Corresponding 33321
The following data on the height and the corresponding number of pupils were found in the measurement of 63 pupils: the height; number of pupils 159cm; 1 161cm; 1 162cm; 2 163cm; 1 164cm; 2 165cm; 2 166cm; 3 167cm; 2 168cm; 4 169cm; 3 170cm; 5 171cm; 6 17 - Rectangular 61183
Mr. Nový exchanged his rectangular plot of 5.2 hectares with his neighbor for two. The first plot has the shape of a square with a side of 70 m, and the second has the shape of a rectangle with dimensions of 110 m and 410 m. After the exchange, does the n - Two gardens
The total area of the two gardens is 864 m². The first garden is 60 m² smaller than three times the second garden. What is the area of each garden?
- Numbers 24281
Of the four numbers, the second is five larger than the first, the third two smaller than the first, and the fourth is twice larger than the first. Find these numbers if their sum is 38. - Std-deviation
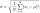Calculate the standard deviation for file: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90 - Two gardens
The flower garden has a square shape. The new garden has a rectangular shape; one dimension is 8 m smaller, and the other is twice as large as in a square garden. What were the original and new garden dimensions if both gardens' areas were the same?
