Refractive index
The light passes through the interface between air and glass with a refractive index of 1.5. Find:
(a) the angle of refraction if light strikes the interface from the air at an angle of 40°.
(b) the angle of refraction when light hits the glass interface at an angle of 40°.
(c) the angle of incidence if the light is refracted at 20° on impact from the glass.
(d) cut-off angle (justify for which way the light passes through the interface)
(a) the angle of refraction if light strikes the interface from the air at an angle of 40°.
(b) the angle of refraction when light hits the glass interface at an angle of 40°.
(c) the angle of incidence if the light is refracted at 20° on impact from the glass.
(d) cut-off angle (justify for which way the light passes through the interface)
Final Answer:

Tips for related online calculators
Check out our ratio calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
basic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Diamond cutoff angle
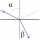 Find the cut-off angle for the diamond-air pair. n_d = 2.42 α_m =? The absolute refractive index of light for air n = 1
Find the cut-off angle for the diamond-air pair. n_d = 2.42 α_m =? The absolute refractive index of light for air n = 1 - Tennis ball parabola
 In a tennis match, Adrien is 5 m from the net when he hits a ball 80 cm off the ground. The maximum height of its parabolic path passing through the net was 1.5 m. If the length of the court is 23.77 m, will the ball land inside the court?
In a tennis match, Adrien is 5 m from the net when he hits a ball 80 cm off the ground. The maximum height of its parabolic path passing through the net was 1.5 m. If the length of the court is 23.77 m, will the ball land inside the court? - Light intensity
 The light beam loses 1/12 of its intensity as it passes through the glass plate. What will the beam's intensity be after passing through a ten times stronger plate?
The light beam loses 1/12 of its intensity as it passes through the glass plate. What will the beam's intensity be after passing through a ten times stronger plate? - The bridge
 Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen sees the bridge from the largest angle?
Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen sees the bridge from the largest angle? - Altitude angle
 In complete winds-free weather, the balloon took off and remained standing exactly above the place from which it took off. It is 250 meters away from us. How high did the balloon fly when we saw it at an altitude angle of 25°?
In complete winds-free weather, the balloon took off and remained standing exactly above the place from which it took off. It is 250 meters away from us. How high did the balloon fly when we saw it at an altitude angle of 25°? - Scalar dot product
 Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120°
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - Isosceles weight
 A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight?
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight?
