From plasticine
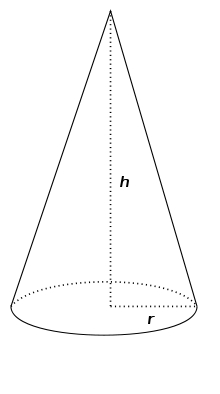
Michael modeled from plasticine a 15 cm high pyramid with a rectangular base, with the sides of the base a = 12 cm and b = 8 cm. From this pyramid, Jane modeled a rotating cone with a base diameter of 10 cm. How tall was Jane's cone?
Your answer:
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cone
The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base? - Pyramid plasticine
The base of the needle is a rectangle with dimensions of 20 cm and 10 cm, its height is 15 cm. Will the plasticine we needed to model this pyramid be enough to model two pyramids with a square base of 10 x 10 cm and a height of 15 cm? - Rectangular base - II
Calculate the volume of a pyramid with a rectangular base with sides a = 7 cm, b = 5 cm, and height of the pyramid v = 13 cm. - Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm. - Rotating cone
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times - Triangle rotation volume
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body. - The volume
The volume of the rotating cone is 376.8 cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
