Miško
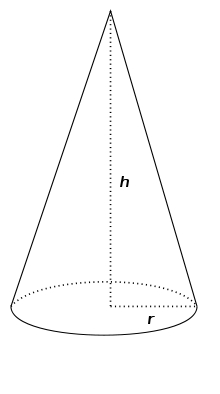
Miško vymodeloval z plastelíny 15 cm vysoký jehlan s obdélníkovou podstavou se stranami podstavy a = 12 cm a b = 8 cm. Janka z tohoto jehlanu vymodelovala rotační kužel s průměrem podstavy d = 10 cm. Jakou výšku měl Jankin kužel?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Vypočítej 390
Vypočítej objem jehlanu s obdélníkovou podstavou o stranách a= 7 cm, b=5 cm a výškou jehlanu v=13 cm - 4b jehlan nepravidelný
Vypočítej povrch čtyřbokého jehlanu, který má obdélníkovou podstavu s rozměry a= 8 cm, b = 6 cm a výšku v = 10 cm. - Rotační 14
Rotační kužel má průměr podstavy 18 dm a výšku 12 dm. Vypočítejte jeho objem V . - Hranol + jehlan
Vypočítejte objem tělesa, které je složeno z hranolu a jehlanu se stejnou čtvercovou podstavou o hraně 8 cm. Hranol je vysoký 20 cm a jehlan 15 cm. - Je dán 21
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15 cm a výškou v=21 cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Velký kužel
Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Jehlan 8
Jehlan s obdélníkovou podstavou o rozměrech 6 dm a 8 dm má boční hranu délky 13 dm. Vypočítejte povrch a objem tohoto jehlanu.
