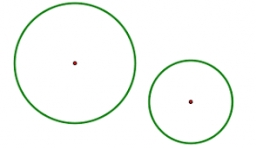
Determine 44221
For circles k1 (S1,4cm) and k2 (S2,3cm) and it holds that | S1S2 | = 8cm. Determine the distance between the circles K1 and K2.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circles
For the circle c1(S1; r1=109 cm) and c2(S2; r2 = 152 cm) is distance of centers |S1S2| = 261 cm. Determine the distance between the circles. - Intersections 68784
The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places. - Two parallel chords
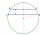In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long. - Quadrilateral 78874
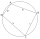Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
- Centimeters 7406
Circles with radii r1 = 10 centimeters and r2 = 4 cm touch from the outside. What is the distance between their centers? - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Isosceles 2588
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
