Resistors
Two parallel resistors connected in series give the resulting resistance $R1Ω and $R2Ω. Determine the resistance of these resistors.
Final Answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsnumbersUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Resistance 6626
 Two resistors of 20 Ω and 30 Ω are connected in the electrical circuit. a, Calculate the total resistance in the electrical circuit if the resistors are connected in series. b, Calculate the total resistance in the electrical circuit if the resistors are
Two resistors of 20 Ω and 30 Ω are connected in the electrical circuit. a, Calculate the total resistance in the electrical circuit if the resistors are connected in series. b, Calculate the total resistance in the electrical circuit if the resistors are - Two conductors
 Two conductors have resistance Rs=5 ohms when connected in series and Rp=1.2 ohms when connected in parallel. Calculate the value of the resistors.
Two conductors have resistance Rs=5 ohms when connected in series and Rp=1.2 ohms when connected in parallel. Calculate the value of the resistors. - Resistance 80577
 Three identical resistors connected in series have a total resistance of 9 ohms. What will be their total resistance when connected in parallel
Three identical resistors connected in series have a total resistance of 9 ohms. What will be their total resistance when connected in parallel - Two resistors 5
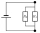 Two resistors are connected in parallel. The first resistor has a resistance of 2000 ohms and a current of 4 mA flows through it. The second resistor has a resistance of 1600 ohms. 1/Draw a circuit diagram 2/Determine the voltage of the power source. 3/Wh
Two resistors are connected in parallel. The first resistor has a resistance of 2000 ohms and a current of 4 mA flows through it. The second resistor has a resistance of 1600 ohms. 1/Draw a circuit diagram 2/Determine the voltage of the power source. 3/Wh - Respective 25361
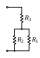 Three resistors are connected according to the scheme (R1 in parallel with R2 and series with R3: R1||R2 + R3) so that R1=0.6 Ω, R2=2 Ω, R3=3 Ω, current I1 = 10 A. Calculate all the currents passing through the respective resistors R1, R2, R3 and all the
Three resistors are connected according to the scheme (R1 in parallel with R2 and series with R3: R1||R2 + R3) so that R1=0.6 Ω, R2=2 Ω, R3=3 Ω, current I1 = 10 A. Calculate all the currents passing through the respective resistors R1, R2, R3 and all the - Resistances 25271
 Three resistors with resistances of 200 Ω, 400 Ω, and 600 Ω are connected in series (in series)—a current of 1.8 A flows through the first 200Ω resistor. a) What current passes through the second and what current through the third resistor? b) What are th
Three resistors with resistances of 200 Ω, 400 Ω, and 600 Ω are connected in series (in series)—a current of 1.8 A flows through the first 200Ω resistor. a) What current passes through the second and what current through the third resistor? b) What are th - Resistance 80351
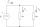 We connected two resistors in parallel in the circuit, with the first having three times the resistance of the second. The voltage between the terminals of each resistor is 6 V. Calculate the current through each branch when the resulting resistance of bo
We connected two resistors in parallel in the circuit, with the first having three times the resistance of the second. The voltage between the terminals of each resistor is 6 V. Calculate the current through each branch when the resulting resistance of bo
