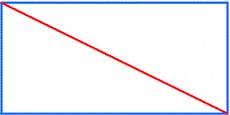
Rectangle 3-4-5
The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- diagonal
- rectangle
- basic functions
- ratio
- direct relationship
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Circumference 7615
The sides of the rectangle are in a ratio of 3:5. Its circumference is 48 cm. Calculate the length of its diagonal. - The sides
The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals - Rectangular 80776
The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden. - Rectangular 7801
The length of the sides of the rectangular garden is 4:3. The junction of the centers of adjacent sides is 20 m long. Calculate the area of the garden. - Ratio of sides
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Rectangular garden
The sides of the rectangular garden are in ratio 1:2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden. - Calculate 70814
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - Rectangular 4624
The lengths of the sides of the rectangular garden are in the ratio of 1: 2. The junction of the centers of adjacent sides is 20 m long. Calculate the perimeter and acreage of the land. - Rectangle - sides 4
The perimeter of the rectangle is 72 cm. Calculate the length of the sides that are in the ratio of 3:5. - Rectangular 6255
The lengths of the sides of the rectangular garden are in the ratio of 1: 2. The connection of the centers of the adjacent sides is 20 m long. Calculate the perimeter and area of the rectangle. - Rectangle 62854
The aspect ratio of the rectangle and its diagonal is 9:12:15. Calculate the area of the rectangle if the length of the diagonal is 105 cm. - Rectangle - desc circle
The length of the sides of the rectangle is at a ratio of 1:3. The circle's radius circumscribed to the rectangle is 10 cm. Calculate the rectangle's perimeter. - Circle and rectangle
The circle describes a rectangle with sides of 11.7 cm and 175 mm. What is its length? Calculate the area of the circle described by this circle. - Rhombus
The rhombus has diagonal lengths of 4.2cm and 3.4cm. Calculate the length of the sides of the rhombus and its height - Circumference 15873
The sides of the triangle are in a ratio of 3:4:6. One side of it measures 21 cm. Calculate its circumference. - Dimensions 20513
The sides of the rectangle are 6.6 cm and 4.2 cm. We change its dimensions in a ratio of 5:2. How many times does the rectangle's area change compare to the original rectangle? - Calculate 2416
In the rectangle ABCD we know the side length AB = 16 cm and the diagonal AC = 20 cm. Calculate its perimeter and area.
