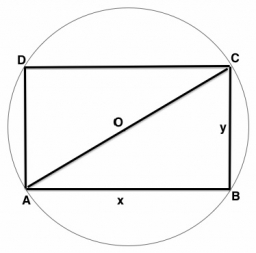
Ratio of sides

Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.

Correct answer:

S =  157.6174 cm²

Step-by-step explanation:

$$\begin{gathered} r=9\text{cm} \\ {r}^2=(a/2{)}^2+(b/2{)}^2 \\ a:b=2:7 \\ {r}^2=(a/2{)}^2+((7/2\cdot a)/2{)}^2 \\ {r}^2=a^2/4+a^2\cdot (7/4{)}^2 \\ a=r/(\sqrt{1/4+(7/4{)}^2})=9/(\sqrt{1/4+(7/4{)}^2})\doteq 4.945\text{cm} \\ b=7/2\cdot a=7/2\cdot 4.945\doteq 17.3074\text{cm} \\ o=2\cdot (a+b)=2\cdot (4.945+17.3074)\doteq 44.5048\text{cm} \\ o=2\pi \cdot r_1 \\ {r}_1=o/(2\pi )=44.5048/(2\cdot 3.1416)\doteq 7.0832\text{cm} \\ S=\pi \cdot r_1^2=3.1416\cdot 7.0832^2=157.6174{\text{cm}}^2 \end{gathered}$$

Try another example