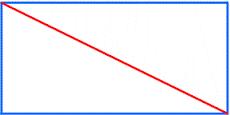
Rectangle
The rectangle has a perimeter of 75 cm. The diagonal length is 32.5 cm. Determine the length of the sides.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Circle and rectangle
The circle describes a rectangle with sides of 11.7 cm and 175 mm. What is its length? Calculate the area of the circle described by this circle. - The sides
The sides of a rectangle are in the ratio 3:5, and its perimeter is 72 cm. Calculate: a) the lengths of both sides of the rectangle, b) the area of the rectangle, c) the length of the diagonals. - Rectangle Diagonal Length
The sides of the rectangle are in a ratio of 3:5. Its circumference is 48 cm. Calculate the length of its diagonal. - Square diagonal
Determine the diagonal of a square whose perimeter is equal to 72 cm. - Rectangle - sides 4
The perimeter of the rectangle is 72 cm. Calculate the length of the sides that are in the ratio of 3:5. - Rectangle
The perimeter of the rectangle is 22 cm, and the area is 30 cm². Determine its dimensions if integers express the length of the sides of the rectangle in centimeters. - Rectangle - sides
One side of the rectangle is 14 cm long. The perimeter of the rectangle is 32 cm. Calculate the length of the other side of the rectangle.
