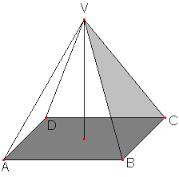
Metal pyramid
Find the weight of a regular quadrilateral pyramid with a 5 cm length and 6,5 cm body height made from material with density g/cm3.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
Tip: Our Density units converter will help you convert density units.
Tip: Our Density units converter will help you convert density units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Quadrilateral 28491
Calculate the weight of a regular quadrilateral pyramid with a base edge of 4 cm in length and a body height of 6 cm if it is made of a material density of 8 g/cm³. - The cast
The cast in the body of a regular quadrilateral pyramid with a base edge 60 cm long and 5 cm high is made of a material with a density of 7.8 g/cm cubic. Calculate its weight. - Pyramid-shaped 15643
The regular quadrilateral pyramid-shaped casting, with a base edge 60 cm in length and 5 cm in height, is made of a material density of 7.8 g / cm 3. Calculate its weight. - Special body
Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body.
- Quadrilateral 40551
Find the volume and surface area of a regular quadrilateral pyramid ABCDV if its leading edge has a length a = 10 cm and a body height h = 12 cm. - Wooden prism
Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³. - Quadrangular pyramid
Given is a regular quadrangular pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area.
