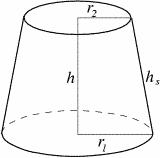
Truncated cone 3
The surface of the truncated rotating cone S = 7697 meters square, the substructure diameter is 56m and 42m, find the height of the tang.
Correct answer:
Tips to related online calculators
Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Cap
Jesters hat is shaped by a rotating cone. Calculate how much paper is needed to the cap 54 cm high when the head circumference is 47 cm. - Truncated cone
Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm and side s = 10 cm. - The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Rotating cone
Find the rotating cone's surface and volume if its side is 150 mm long and the circumference of the base is 43.96 cm. - Frustrum - volume, area
Calculate the surface and volume of the truncated cone, the radius of the smaller figure is 4 cm, the height of the cone is 4 cm and the side of the truncated cone is 5 cm. - Church roof 2
The roof has the shape of a rotating cone shell with a base diameter of 6 m and a height of 2.5 m. How many monez (CZK) will cost the roof cover sheet if 1 m² of metal sheet costs 152 CZK and if you need 15% extra for joints, overlays and waste? - Top-open tank
The top-open tank has the shape of a truncated rotating cone, which stands on a smaller base. The tank's volume is 465 m3, the radii of the bases are 4 m and 3 m. Find the depth of the tank. - Truncated cone 6
Calculate the volume of the truncated cone whose bases consist of an inscribed circle and a circle circumscribed to the opposite sides of the cube with the edge length a=1. - Truncated pyramid
Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, height v = 8 cm. - Traffic cones
Forty identical traffic cones with a base diameter d = 3 dm and a height v = 6 dm should be painted on the outside with orange paint (without base). How many crowns do we pay for color? If we need 50 cm ^ 3 of paint to paint, 1m² and 1l of paint costs CZK - Slant height 2
A regular triangular pyramid with a slant height of 9 m has a volume equal to 50 m³. Find the lateral area of the pyramid. - A concrete pedestal A concrete pedestal has a shape of a right circular cone having a height of 2.5 feet. The diameter of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the lateral surface area, total surface area, and the volume of the pedestal.
- Truncated cone
A truncated cone has bases with radiuses of 40 cm and 10 cm and a height of 25 cm. Calculate its surface area and volume. - Frustum of a cone
A reservoir contains 28.54 m³ of water when full. The diameter of the upper base is 3.5 m, while at the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Rotary bodies
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height v = 15 cm. Which of these two bodies has a larger surface area? - Truncated cone
Calculate the height of the rotating truncated cone with volume V = 1354 cm³ and a base radii r1 = 9.1 cm and r2 = 5.4 cm. - Angle of deviation
The surface of the rotating cone is 30 cm² (with circle base), its surface area is 20 cm². Calculate the deviation of the side of this cone from the plane of the base.
