Komolý kužel
Povrch komolého rotačního kužele S = 7697 m čtverečních, průměry podstav jsou 56 m a 42 m, určete výška kužele.
Vaše odpověď:
Vaše odpověď:
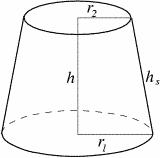
Tipy na související online kalkulačky
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Lampa
Vypočtěte povrch lampového stínítka tvaru rotačního komolého kužele s průměry podstav 32 cm a 12 cm a výškou 24 cm. - Komolý kužel
Vypočítejte povrch a objem komolého rotačního kužele s poloměry podstav 8 cm a 4 cm a výšce 5 cm. - Povrch
Povrch komolého rotačního kužele se stranou s = 13 cm je S = 510π cm². Urči poloměry podstav, když je rozdíl délek je 10 cm. - Povrch 32
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Rot kužel
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=2,3 dm a výškou v=46 mm. - Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r1=19 cm, r2 = 6 cm a výškou v = 22 cm. - Shora
Shora otevřená nádrž má tvar komolého rotačního kužele, který stojí na menší podstavě. Objem nádrže je 465 m3, poloměry podstav jsou 4 m a 3 m. Vypočítejte hloubku nádrže.
