Tangent 3
In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm.
Correct answer:
Showing 3 comments:
Tips for related online calculators
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Applies 14683
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - MO circles
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Chord BC
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates: [- 14; 0]? - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Two chords
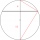Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Calculate 79144
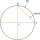The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Concentric 18343
Construct three concentric circles k, l, m with center at point S and with radii 2cm, 3cm, and 40mm - The rectangle 5
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r - Instructions: 56651
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles). - Chord
It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB. - Katy MO
Kate drew a triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4 - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Connect 6500
Draw the line KL = 55mm. Draw a circle k with center K and radius 4cm. Mark the points to belong to the circle and connect them with point L. - Circle tangent
It is given to a circle with the center S and a radius of 3.5 cm. The distance from the center to line p is 6 cm. Construct a circle tangent n which is perpendicular to the line p. - Find the 5
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Sin cos tan
In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C.
